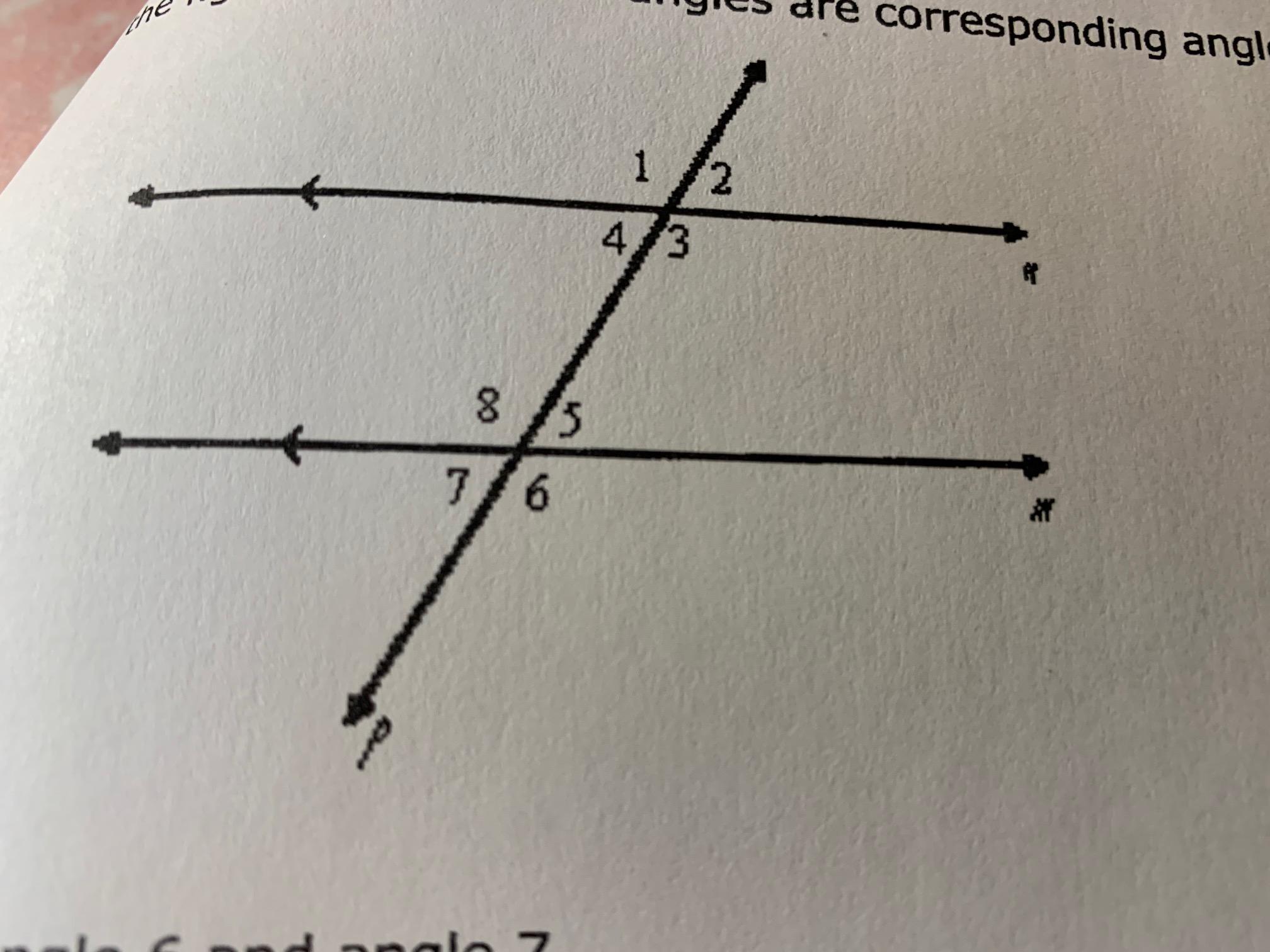
In the figure, what set of angles are corresponding angles?angle 6 and angle 7angle 5 and angle 7angle 1 and angle 7angle 4 and angle 7
Answers
Step 1
In geometry, corresponding angles are formed where a line known as an intersecting transversal, crosses through a pair of straight lines. Corresponding angles are the pairs of angles that are found in the same relative position on different intersections.
Step 2
Find the set of corresponding angles
[tex]\text{Angle 4 and angle 7}[/tex]Hence, the set of corresponding angles is; angle 4 and angle 7
Related Questions
helpppppp!!!!!!!!!!!!!!!!!!!!
Answers
Answer
D. Observations of constellations show that stars have moved over time.
Explanation:
A scientific claim is basically an observation in science.
Constellation changes there position over time because of earth's rotation around sun. So, observation of constellations shows that stars have moved over time is a scietific claim. If stars would not move then constellation will not form.
solve for rv=r+at, for r
Answers
Since we need to solve for r we have to leave that variable alone in one side of the equation. We notice that at is adding in the right side, then it goes to the left side substracting, that is:
[tex]v-at=r[/tex]Therefore:
[tex]r=v-at[/tex]in the last part we only switch the sides of the equation.
In ACDE, J is the centroid. If JG=21 find CG. D F G C E H
Answers
Let's begin by identifying key information given to us:
We have triangle CDE
J is the centroid
[tex]\begin{gathered} JG=21 \\ \text{The centroid of a triangle divides }\frac{2}{3\text{ }}\text{the distance from}verte\text{x to midpoint of the sides} \\ \Rightarrow JG=\frac{2}{3}CG \\ \Rightarrow21=\frac{2}{3}CG=\frac{63}{2} \\ \therefore CG=\frac{63}{2}=31.5 \end{gathered}[/tex]following: Find the locus of points whose: ordinate is 1 greater than twice the abscissa
Answers
ordinate is 1 greater than twice the abscissa :
[tex]\begin{gathered} x=abscissa \\ y=ordinate \\ y=2x+1 \end{gathered}[/tex]Can You Teach Me How To Multiple Fractions ?
Answers
Let's suppose we are given two fractions:
[tex]\frac{a}{b},\frac{c}{d}[/tex]In order to multiply them we simply multiply the numerators and denominators, like this:
[tex]\frac{a}{b}\times\frac{c}{d}=\frac{a\times c}{b\times d}[/tex]For example, let's say we are given the following fractions:
[tex]\frac{1}{2},\frac{3}{5}[/tex]We can multiply them following the previous rule:
[tex]\frac{1}{2}\times\frac{3}{5}=\frac{1\times3}{2\times5}=\frac{3}{10}[/tex]find the equation of the circle with the given center and radius:center (-1,-6), and radius = 6
Answers
ANSWER:
[tex](x+1)^2+(y+6)^2=36^{}[/tex]STEP-BY-STEP EXPLANATION:
We have that the equation of the circle is given as follows:
[tex]\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ \text{where (h, k) is the center and r is the radius } \end{gathered}[/tex]Replacing:
[tex]\begin{gathered} (x-(-1))^2+(y-(-6))^2=6^2 \\ (x+1)^2+(y+6)^2=36^{} \end{gathered}[/tex]How many different committees can be formed from 12 teachers and 32 students if the committee consists of 3 teachers and 2 students?
Answers
Answer: 4 committees
Step-by-step explanation:
12 divided by 3 = 4 (this equation represents the teachers)
2 x 4 = 8 (this equation represents the students)
There can only be 4 committees because there are only 12 teachers. There are some students that will not be in a committee. 24 students will be committee-less to be exact.
If each quadrilateral below is a square, find the missing measure
Answers
ANSWER
[tex]x=11[/tex]EXPLANATION
The figure given is a square.
Each angle in a square is 90 degrees and the diagonals bisect each angle.
This means that :
[tex]\begin{gathered} 6x-21=45 \\ \text{Collect like terms:} \\ 6x=45+21 \\ 6x=66 \\ \text{Divide through by 6:} \\ x=\frac{66}{6} \\ x=11 \end{gathered}[/tex]That is the value of x.
This is very hard for me I need to know how to do it
Answers
The zeros of a function are the values of x that make the function be equal to zero.
When graphing a quadratic equation, the graph is a parabola, and the zeros of the function are the x-intercepts of the graph, which are the points where the graph intersects the x-axis.
So, if the zeros of this function are x = -8 and x = 2, that means the parabola crosses the x-axis at x = -8 and x = 2.
Therefore the correct option is the first one.
1: 9 11. The cost for a group of people to go to the movies is given by the expression 9a + 5b, where a is the number of adults and b is the number of children. What are the variables of this expression? of of A. 9 and 5 B. a and b C. 9a and 5b D. + and x
Answers
the variables are
a and bwhere
a -----> is the number of adults
b-------> is the number of children.
answer is option B
Y=1/3x+2 standard form
Answers
3y - x = 6 is standard form for the given equation
What is standard form of linear equation ?The typical form for linear equations with two variables is Ax+By=C.For instance, the linear equation 2x+3y=5 is in standard form. Finding both intercepts of an equation in this style is quite easy (x and y).This form is also very useful when trying to solve systems of two linear equations.Calculationy = 1/3x + 2
3y = x + 6
3y - x = 6 is standard form
learn more about standard form of linear equation here :
brainly.com/question/17264364
#SPJ4
8) Remus earns $.15 per unit for the work he does. For all units heproduces in a week, over 1,000, he receives $.20. What were his weeklyearnings if he produced 1,420 units?
Answers
You have the following information:
- Remus earns $.15 per unit
- For units he produced over 1,000 he receives $.20
- He produced 1,420 units
In order to determine what were the weekly earnings, you first take into account the earnings for the first 1,000 units:
0.15 x 1,000 = 150
Next, you calculate the earnings for the units over 1,000, which are 420:
0.20 x 420 = 84
Next, you sum both contributions:
150 + 84 = 234
Hence, the weekly earning os Ramus were of $234
Cindy eats 12 oz of candy in 4 days how long will it take her to eat 1 pound of candy
Answers
We should know that:
1 pound = 16 oz
given Cindy eats 12 oz in 4 days
She will eat 1 pound in x days
So, we need to find the number of days to eat 1 pound which is equal to 16 oz
Using the ratio and proportion
12 : 4 = 16 : x
[tex]\begin{gathered} 12\colon4=16\colon x \\ \frac{12}{4}=\frac{16}{x} \\ x=\frac{4\cdot16}{12}=\frac{16}{3}=5\frac{1}{3} \end{gathered}[/tex]so, the number of days = 5 1/3
Write each ratio using the given figure. If necessary, find the missing side.Tan P = ___________Answer?
Answers
Hello!
First, let's analyze the figure and write each side:
Analyzing it, we don't have enough information yet to calculate the tangent (because we don't know the measurement of P).
So, let's calculate the opposite side (by Pithagoras):
[tex]\begin{gathered} a^2=b^2+c^2 \\ 41^2=40^2+c^2 \\ 1681=1600+c^2 \\ 1681-1600=c^2 \\ c^2=81 \\ c=\sqrt{81} \\ c=9 \end{gathered}[/tex]As we know the opposite side, we can calculate the tangent of P, look:
[tex]\begin{gathered} \tan(P)=\frac{\text{ opposite}}{\text{ adjacent}} \\ \\ \tan(P)=\frac{9}{40} \\ \\ \tan(P)=0.225 \end{gathered}[/tex]Curiosity: using the trigonometric table, this value corresponds to approximately 13º.
Answer:The tangent of P is 0.225.
Convert the binary number ( 365.24 ) into decimal number.
Answers
Given:
The given deciaml number is 365.24.
Required:
We need to convert the given decimal number into a binary number.
Explanation:
Consider the integer part of the given number.
[tex]365[/tex]Divide the number 365.
Consider the fraction part of the given number.
[tex]0.24[/tex]Multiply the number 0.24 by 2.
The binary number of the decimal number is
[tex]365.24_{10}=101101101.0011110101_2[/tex]Final answer:
[tex]101101101.0011110101[/tex]Christine is a software saleswoman. Let y represent her total pay (in dollars). Let x represent the number of copies of Math is Fun she sells. Suppose that x and y are related by the equation 70x + 1700= y.Answer the questions below. Note that a change can be an increase or a decrease. For an increase, use a positive number. For a decrease, use a negative number. What is the change in Christine’s total pay for each copy of Math is Fun she sells? What is Christine’s total pay if she doesn’t sell any copies of Math is Fun?
Answers
From the information given, the equation relating her total pay (in dollars), y to the number of copies of Math is Fun she sells, x is expressed as
y = 70x + 1700
This is a linear equation. The slope intercept form of a linear equation is expressed as
y = mx + b
where
m = slope or rate of change
b = y intercept of the value of y when x = 0
By comparing both equations,
m = 70
b = 1700
a) Thus, the change in Christine’s total pay for each copy of Math is Fun she sells 70 dollars per copy
b) Christine’s total pay if she doesn’t sell any copies of Math is Fun is the value of y when x = 0. thus,
Christine’s total pay if she doesn’t sell any copies of Math is Fun = $1700
Carmen has 12 loaves of pumpkin bread. She cuts each loaf into 1/8 pieces and gives one piece to each of her friends. How many friends can Carmen give a piece of pumpkin bread?
Answers
12 loaves of pumpkin bread.
Each loave is cut into 1/8 pieces.
So, there are 8 pieces per loaf:
8 pieces per loaf x 12 loaves = 96 pieces
If she gives one piece to each friend she can give it to 96 friends:
96 pieces / x friends = 1 per friend
96/x =1
96 = x(1)
96= x
30-28-25-21-16 next number
Answers
Answer:
10
Step-by-step explanation:
30 -2
28 -3
25 -4
21 -5
16 -6
= 10
Answer:
10
Step-by-step explanation:
Given the sequence 30, 28, 25, 21, 16, you want to know the next number.
DifferencesFirst differences between successive terms are ...
28 -30 = -2
25 -28 = -3
21 -25 = -4
16 -21 = -5
These are not constant, so this is not an arithmetic sequence. However, we notice the second differences are constant:
-3 -(-2) = -1
-4 -(-3) = -1
-5 -(-4) = -1
ApplicationThis observation tells us the next second difference is ...
-5 +(-1) = -6
And the next number in sequence is ...
16 +(-6) = 10
The next number is 10.
__
Additional comment
When a sequence of numbers is described by a polynomial or exponential, looking at differences (and their differences) can help determine the degree of the polynomial, or the common ratio of the exponential.
Here, the second differences are constant, so a second-degree (quadratic) polynomial will describe the sequence. The polynomial describing this sequence is ...
a(n) = 31 -(n)(n+1)/2
A radio announcer asked her listeners which type of music they preferred. The results are below. which answer choice lists the results from greatest to least perefence?F. 0.10, 25%, 0.20, 45/100G. 25%, 45/100, 0.20, 0.10H. 0.10, 0.20, 25%, 45/100J. 45/100, 25%, 0.20, 0.10
Answers
To compare the preferences is best to express them using the same form, for example, express all values as decimal values:
To express 25% as a decimal value you have to divide it by 100:
[tex]\frac{25}{100}=0.25[/tex]To express the fraction 45/100 as a decimal value you have to divide 45 by 100
[tex]45\div100=0.45[/tex]So, the observations expressed as decimal values are:
Rap 0.25
Norteno 0.45
Kazz 0.20
Tejano 0.10
Now that all numbers are on the same form you can order them from greatest to least. To do so, you have to compare the digit on the first decimal place, if the first digit is equal, you have to compare the digit on the second decimal place.
The number with the greatest decimal value is 0.45
Then you have 0.20 and 0.25 both have the same first digit, so you have to compare the second digits. "0" is less than "5" so, 0.20 is less than 0.25.
The least value is 0.10.
So ordered from greatest to least the values are:
[tex]\begin{gathered} 0.45;0.25;0.20;0.10= \\ \frac{45}{100};25\%,0.20;0.10 \end{gathered}[/tex]The correct option is J.
The equation of a line that is perpindicular to y=10x but passes through (1, -3)
Answers
The equation of line is y = -x/10 + -29/10.
Given,
The equation of a line that is perpendicular to y = 10x
and, passes through the (1, -3)
To find the equation of line.
Now, According to the question:
Find the slope of the line that is perpendicular to y = 10x;
m = - 1/10
We know that, Slope of line is ;
y = mx + c
m = -1/10
x = 1
y = -3
Substitute and calculate
- 3 = -1/10 + b
b = -29/10
Now, y = mx + b
Substitute all the values in above slope equation:
y = -x/10 + -29/10
Hence, The equation of line is y = -x/10 + -29/10.
Learn more about Equation of line at:
https://brainly.com/question/21511618
#SPJ1
All lines that cross the x-axis are vertical lines.A. TrueB. False
Answers
Given:
All lines that cross the x-axis are vertical line.
Required:
To find whether the given statement is true or false.
Explanation:
A vertical line is one the goes straight up and down, parallel to the y-axis of the coordinate plane.
The x-intercept is the point at which the graph crosses the x-axis.
Here all lines are not vertical lines.
Therefore the given statement is false.
Final answer:
False.
The number of books he collects, n, is defined by n = 140 + 21 where d is the number of days he spends collectingRobert is collecting books to donate to the library.books.What does 14 represent in the context of Robert's book collecting?A represents the number of books per day that are collected,® represents the number of books per week that are collected.represents the number of books per month that are collected.o represents the number of books per year that are collected.
Answers
The equation for number of books collected by Robert is given as;
n= 14 d + 21
where d is the number of days he spent collecting .
Answer A. represents the number of books per day that are collected
write an equation in slope -intercept form for the line with y- intercept -1 and slope -3/2
Answers
The line equation in the slope -intercept form can be written as,
[tex]y=mx+b[/tex]Here, m is the slope and b is the y intercept.
Given,
m = -3/2 and b = -1, therefore we can write the equation as,
[tex]y=-\frac{3}{2}x-1[/tex]The equation is, y =(-3/2)x-1.
Select the polynomial functions for which (x+3) is a factor. Select all that apply.
Answers
If x+3 is a factor, then the result of replacing x=-3 in each equation would be 0.
Replacing x=-3 in the polynomials, we have:
Option A
[tex]\begin{gathered} f(-3)=(-3)^4-12(-3)^3+54(-3)^2-108(-3)+81=1296\text{ } \\ \text{ We see that option A is incorrect.} \end{gathered}[/tex]Option B
[tex]\begin{gathered} f(-3)=(-3)^4-3(-3)^3-(-3)+3=168\text{ } \\ \text{We see that option B is incorrect.} \end{gathered}[/tex]Option C
[tex]\begin{gathered} f(-3)=(-3)^5+2(-3)^4-23(-3)^3-60(-3)^2=0\text{ } \\ \text{We see that option C is correct.} \end{gathered}[/tex]Option D
[tex]\begin{gathered} f(-3)=(-3)^5+5(-3)^4-3(-3)^3-29(-3)^2+2(-3)+24=0\text{ } \\ \text{We see that option D is correct.} \end{gathered}[/tex]The answers are options C and D.
3. If you ordered a pizza to share with others, which of the following sets ofnumbers would best describe the part of the pizza you ate.a. Integerb. WholeC. Naturald. Rational
Answers
rational, because you've split the pizza
So for example if you cut the pizza into 12 pieces to one of your friends you gave 1/12
There are 2 liters of soda left after a class party. Laura, Gavin, Anita, Emmett, and Rebecca are on the clean-up crew, and decide to split the soda equally.
How much soda does each student get?
Write your answer as a proper fraction or mixed number.
Answers
0.4 liters or 2/5
Step-by-step explanation:
Dividing the soda equally, Each student would get 0.4 liters or 2/5
Kentaro mixed 3.5 gallons of cranberry juice with 3 quarts of orange juice to make a punch.1 gallon = 4 quarts1 gallon = 16 cups1 cup = 8 fluid OuncesHow many fluid ounces of punch did Kentaro make? Enter the answer in the box.
Answers
The total volume made is 544 fluid ounces of punch
Here, we want to get the amount of fluid ounces of punch made
What we have to do here is to convert each of the volumes to fluid ounces and add together
From the Cranberry juice;
[tex]\begin{gathered} 1\text{ gallon = 16 cups} \\ 3.5\text{ gallons will be = 3.5 }\times\text{ 16 = 56 cups} \\ 1\text{ cup = 8 fluid oz} \\ 56\text{ cups will be; 56}\times\text{ 8 = 448 fluid oz} \end{gathered}[/tex]Now, for the orange juice;
[tex]\begin{gathered} 1\text{ gallon = 4 quarts} \\ 4\text{ quarts = 16 cups} \\ 3\text{ quarts = }\frac{3\times16}{4}\text{ = 12 cups} \\ \\ 1\text{ cup = 8 fluid oz} \\ 12\text{ cups = 12 }\times\text{ 8 = 96 fluid oz} \end{gathered}[/tex]Here, to get the total number, we simply add
That will be;
[tex]96\text{ + 448 = 544 fluid ounces}[/tex]Rewrite the fallowing as an exponential expression in simplest form.
Answers
SOLUTION
[tex]\begin{gathered} 5x\sqrt[]{x} \\ 5x\times\sqrt[]{x} \\ 5x^1\times x^{\frac{1}{2}} \\ 5x^{1+\frac{1}{2}} \\ 5x^{\frac{3}{2}} \\ \end{gathered}[/tex]Solve the system of linear equations by substitution:x - y = -2 and 3x - y = 2
Answers
To solve the system by substitution, isolate one variable from one equation and substitute the expression obtained for that variable into the other equation.
[tex]\begin{gathered} x-y=-2 \\ 3x-y=2 \end{gathered}[/tex]Isolate x from the first equation:
[tex]\begin{gathered} x-y=-2 \\ \Rightarrow x=y-2 \end{gathered}[/tex]Substitute x=y-2 into the second equation:
[tex]\begin{gathered} 3x-y=2 \\ \Rightarrow3(y-2)-y=2 \end{gathered}[/tex]Solve for y:
[tex]\begin{gathered} \Rightarrow3y-6-y=2 \\ \Rightarrow2y-6=2 \\ \Rightarrow2y=2+6 \\ \Rightarrow2y=8 \\ \Rightarrow y=\frac{8}{2} \\ \Rightarrow y=4 \end{gathered}[/tex]Substitute y=4 into the expression of x to find its value:
[tex]\begin{gathered} x=y-2 \\ \Rightarrow x=4-2 \\ \Rightarrow x=2 \end{gathered}[/tex]Therefore, the solution to the given system is:
[tex]\begin{gathered} x=2 \\ y=4 \end{gathered}[/tex]Consider the circle x ^ 2 + y ^ 2 = 100 and the line x + 3y = 10 and their points of intersection (10, 0) and B = (- 8, 6) . Find coordinates for a point C on the circle that makes chords AB and AC have equal length . Be sure to justify your answer.
Answers
The equation of circle is given by,
[tex]x^2+y^2=100\text{ ---(1)}[/tex]The equation of line is given by,
[tex]x+3y=10\text{ ---(2)}[/tex]The points of intersection of the circle and line is,
A=(Xa, Ya)=(10, 0)
B=(Xb, Yb)=(-8, 6)
The length of chord AB can be calculated using distance formula as,
[tex]\begin{gathered} AB=\sqrt[]{(X_b-X_a)^2+(Y_b-Y_a)^2} \\ =\sqrt[]{(-8-10)^2+(6-0)^2} \\ =\sqrt[]{(-18)^2+6^2} \\ =\sqrt[]{324+36} \\ =\sqrt[]{360} \\ =6\sqrt[]{10} \end{gathered}[/tex]Let (Xc, Yc) be the coordinates of point C on the circle. Hence, using equation (1), we can write
[tex]X^2_c+Y^2_c=100\text{ ---(3)}[/tex]Using distance formula, the expression for the length of chord AC is given by,
[tex]AC=\sqrt[]{(X_c^{}-X_a)^2+(Y_c-Y_a)^2_{}}[/tex]Since (Xa, Ya)=(10, 0),
[tex]\begin{gathered} AC=\sqrt[]{(X^{}_c-10_{})^2+(Y_c-0_{})^2_{}} \\ AC=\sqrt[]{(X^{}_c-10_{})^2+Y^2_c} \end{gathered}[/tex]It is given that chords AB and AC have equal length. Hence, we can write
[tex]\begin{gathered} AB=AC \\ 6\sqrt[]{10}=\sqrt[]{(X^{}_c-10_{})^2+Y^2_c} \end{gathered}[/tex]Squaring both sides of above equation,
[tex]\begin{gathered} 360=(X^{}_c-10_{})^2+Y^2_c\text{ } \\ (X^{}_c-10_{})^2+Y^2_c=360\text{ ----(4)} \end{gathered}[/tex]Subtract equation (4) from (3) and solve for Xc.
[tex]\begin{gathered} (X^{}_c-10_{})^2-X^2_c=360-100 \\ X^2_c-2\times X_c\times10+100-X^2_c=260 \\ -20X_c=260-100 \\ -20X_c=160 \\ X_c=\frac{160}{-20} \\ X_c=-8 \end{gathered}[/tex]Put Xc=-8 in equation (3) to find Yc.
[tex]\begin{gathered} (-8)^2+Y^2_c=100 \\ 64+Y^2_c=100 \\ Y^2_c=100-64 \\ Y^2_c=36 \\ Y^{}_c=\pm6 \\ Y^{}_c=6\text{ or }Y_c=-6 \end{gathered}[/tex]So, the coordinates of point C can be (Xc, Yc)=(-8, 6) or (Xc, Yc)=(-8, -6).
Since (-8, 6) are the coordinates of point B, the coordinates of point C can be chosen as (-8, -6).
Therefore, the coordinates of point C is (-8, -6) if chords AB and AC have equal length.