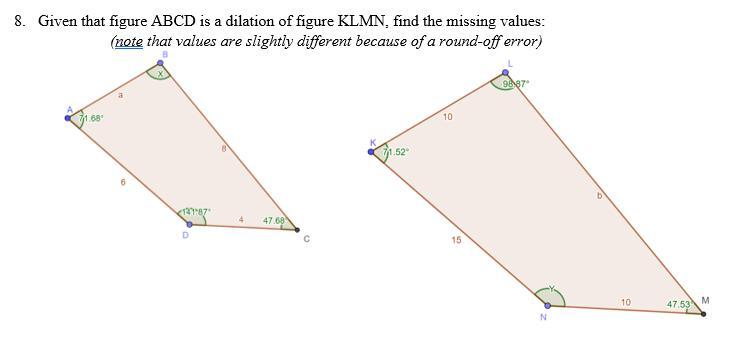
Given that figure ABCD is a dilation of figure KLMN, find the missing values:(note that values are slightly different because of a round-off error)

Part A.

Ethan's account can be model as a linear equation since it is increasing at a constant rate of the form:

And Evan's account can be model as a exponential equation of the form:

Part B:

Evaluate the 1st and 2nd equation for x = 5:

It would be 1.05 higher

Explanation:

If we graph this parabola we can see the vertex at point (4, 16)

The axis of simmetry is a vertical line that passes through the vertex of the parabola.

Any vertical line's equation is:

'a' is any value of x.

Answer:

The equation of the axis of simmetry is x = 4

For them, let x = number of children of the party and

A=Adventure Plext cost

B= Bright Child cost

C= Chuck E Cheese cost

So,

Then, graphing each equation of the system of equations

Now, for determine the break even point for Chuck E Cheese and Bright Child you have

That is, the break even point for Chuck E Cheese and Bright Child occurs when x = 60 children.

For determine the break even point for Adventure Plex and Bright Child you have

That is, the break even point for Adventure Plex and Bright Child occurs when x = 40 children.

Finally, For determine the break even point for Adventure Plex y Chuck E Cheese you have

That is, the break even point for Adventure Plex and Chuck E Cheese occurs when x = 50 children.

Answer:

A population is the entire group that you want to draw conclusions about.

So, in this exercise, the population is all the students attending the college.

Explanation

We are asked to find the total annual budget given that the combined amount for sales and editorial is $12,500,000

To do so, let the total combined amount be x

If we check for the combined percentages for the amount for sales and editorial, we will have

Thus, we can set up the equation

Solving for x

Therefore, the total annual budget will be $50,000,000

The fraction that represent the point A is -1/4.

Since there are 4 divition in between -1 and 0.

Thus the length of one division is,

ANSWER

4,410

EXPLANATION

The number of ways we can choose 4 teachers from 7 teachers is,

There are 35 ways of choosing 4 teachers out of 7.

And the number of ways we can choose 4 students from 9 students is,

There are 126 ways of choosing 4 students out of 9.

The committee is formed by 4 teachers and 4 students. The number of ways it can be made is,

Hence, there are 4,410 ways to choose 4 students and 4 teachers out of 9 students and 7 teachers.

Your calculator uses base 10 for its logs

There should be a button that says log

That is a base 10 log

log 6 = .77815125

To 3 decimal places

log 6 = .778

The base 10 is implied

Answer:

10

Step-by-step explanation:

I divided 570 by 15 to see how many miles she can travel per gallon of gas which came out to be 38.

After that i divided the 380 by the 38. 380÷38 is 10.

Answer:

Need:

10 gallons

Step-by-step explanation:

Proportions:

15 gallons ⇒ 570 miles

A gallons ⇒ 380 miles

A = 15gallons * 380miles / 570miles

A = 10 gallons

Opposite angles are the same

Then:

So: (Remember the line has a 180º degrees

Using the formula for the compound interest, we have:

In this case, we'll have to carry out several steps to find the solution.

Step 01:

Data:

2x - 8 < 7

Step 02:

inequality:

2x - 8 < 7

2x - 8 + 8 < 7 + 8

2x / 2 < 15 / 2

x < 15 / 2

The answer is:

x < 15 / 2

(-oo , 15/2)

The z-score is given by the following formula:

Where x is the data point, μ is the mean, and σ is the standard deviation.

First

The domain of a function is always represented by the values of X. In the ordered pair, they are always the first value of the pair.

The domain is the first number of each pair.

Domain: {-1, -10, 8, 6}.

Answer:

[tex]\frac{1}{12}[/tex]

Step-by-step explanation:

If the brother took home 4/6, that means that you still have 2/6.

[tex]\frac{1}{4}[/tex] x [tex]\frac{2}{6}[/tex] = [tex]\frac{2}{24}[/tex] which is the same as 1/12

Answer:

the answer is 12

Step-by-step explanation:

In short, a = 6 and b = 6. We can make a table of various values to help confirm that 12 is the smallest sum.

Answer: 1

Step-by-step explanation: 1 is the least possible answer because an integer is any number and 1x36 would be the least possible answer for the product.

As we can see we have a horizontal line, the slope of the horizontal line is zero

the form of the equation of the line in slop-intercept form is

where m is the slope and b is the y-intercept.

In our case m=0

in this case the y-intercept is b=-4

Therefore the equation is

ANSWER

y=-4

- 5x + 4 > 19

1st step let us move 4 to the other side by subtracting both sides by 4

- 5x + 4 - 4 > 19 - 4

- 5x > 15

2nd step is move - 5 to the other side by dividing both sides by -5, BUT when we divide the sides of an inequality by a negative number we must reverse the sign of inequality

x < -3

The solution is all values smaller than -3

On the number, line draw an empty circle at -3 then draw from it an arrow pointing to the left ( - ve infinity)

The solution is {x : x < -3} or (-00, -3)

Answer:

[tex]x^{4}[/tex]

Step-by-step explanation:

Whenever it comes to the division of the same variable, we subtract their powers in order to get the correct answer:

[tex]x^{9}/x^{5}[/tex]
[tex]x^{9-5}[/tex]
[tex]x^{4}[/tex]

We are given a problem that can be solved using a system of linear equations. Let A, be the number of adults, and S the number of students. Since there are in total 142 people and there were two days, this means that the sum of the number of adults and the number of students must be 284, which can be written mathematically as follows:

This is our first equation. The second equation is found using the total sales of $1948. Since the ticket per adult is $8 and per student is $5, we have the following equations:

To solve this equation we will solve for A in equation (1), by subtracting S to both sides;

Now we will replace this value in equation (2):

Now we will apply the distributive property:

Addins like terms:

Subtracting 2272 to both sides;

Dividing both sides by -3:

Now we replace this value in equation (1), where we have already solved for A:

Therefore, there were sold 108 student tickets and 140 adult tickets.

In order to find the equation that passes through both points, we can use the slope-intercept form of the linear equation:

Where m is the slope and b is the y-intercept.

Using the given points on this equation, we have:

Therefore the equation is y = -x + 4 (correct option: C)

Given: The function below

To Determine: The range and the graph of g

Solution

The range is as given below

Hence, the range is

{-8, -5, -2, 1}

Let us form a table showing the domain(x) and the range (g(x))

Let us use the table to plot graph of the domain(x) against the range(g(x)) as below

1) Since the sum of these angles is written in terms of x, we can write it out:

Notice that to sum these fractions we had to take the LCM(2, 1) = 2 and rewrite it as a sum.

2) Another way of writing the sum of these angles is writing it as a sum of decimal numbers since we can rewrite fractions as decimal numbers.

3/2 = 3÷2 = 1.5

1/2 = 1÷2 =0.5

1

ANSWER:

STEP-BY-STEP EXPLANATION:

We have the following square root

We calculate by means of the divide and average method.

The first thing is to look for exact roots between those two values

Step 1 estimate

Step 2 divide

Step 3 average:

Therefore: