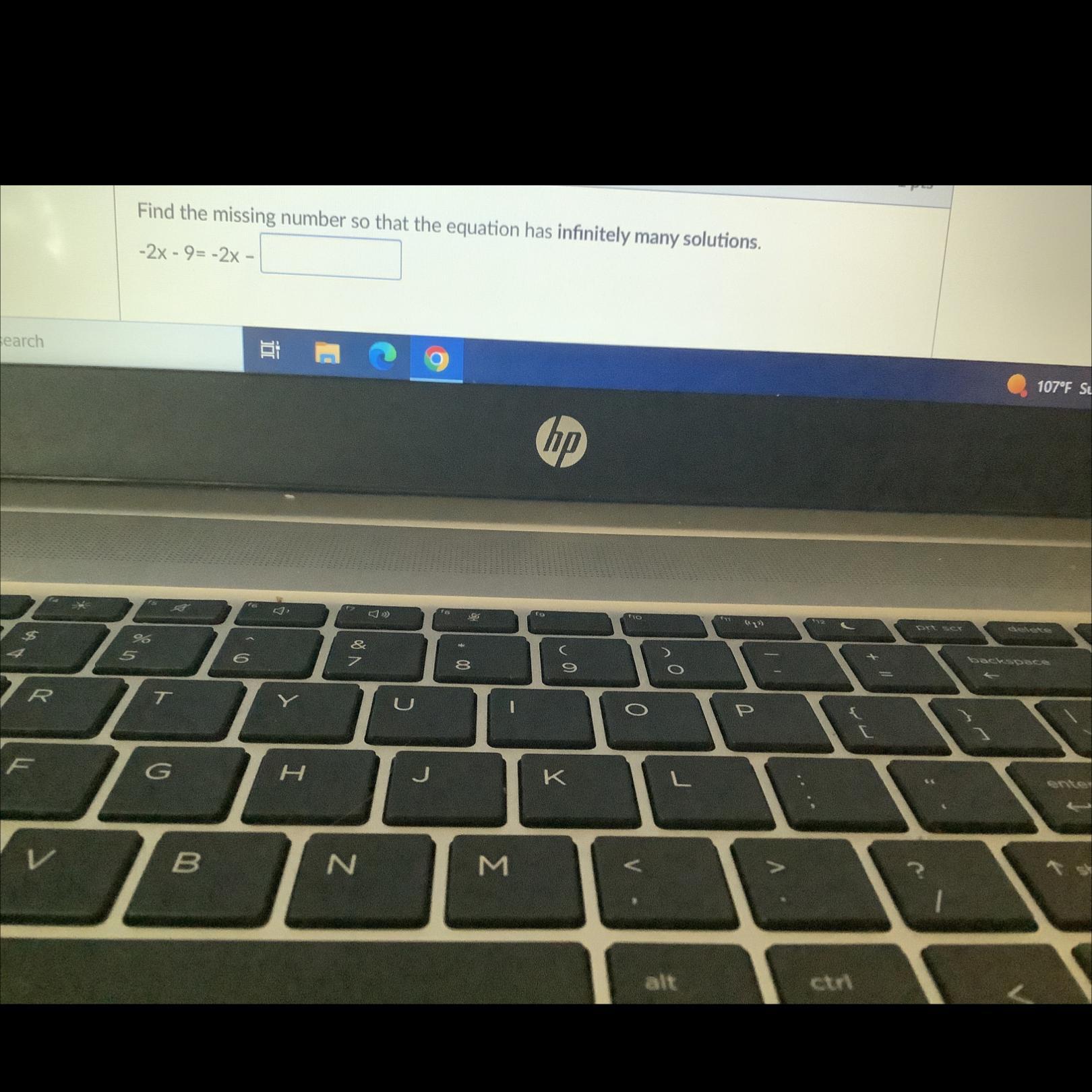
Answers
we have the equation
-2x-9=-2x-?
Remember that
If in a system of two linear equations, we have two identical lines
then
The system has infinite solutions
therefore
the missing number is 9
-2x-9=-2x-9Related Questions
Translate the sentence into an equation,The sum of 5 times a number and 4 is 3.Use the variable b for the unknown number.
Answers
Given the sentence, the sum of 5 times a number and 4 is 3.
The information would translate to;
[tex]\begin{gathered} (5\times b)+4=3 \\ 5b+4=3 \end{gathered}[/tex]ANSWER:
[tex]5b+4=3[/tex]A ball is kicked up in the air from the ground. The height of the ball can be modeled as a function of time in seconds. This function is represented on the graph below. Enter the average rate of change for the height of the ball, measured as feet per second, between 0 seconds and 2 seconds._[blank]_ feet per secondEnter your answer as a number, like this: 42
Answers
ANSWER:
2
STEP-BY-STEP EXPLANATION:
The average rate of change is given by the following formula:
[tex]r=\frac{f(b)-f(a)}{b-a}[/tex]Since it is between 0 and 2 seconds, the values of a and b will be these respectively, the evaluated values can be determined by the graph, therefore:
[tex]\begin{gathered} r=\frac{4-0}{2-0}=\frac{4}{2} \\ \\ r=2\text{ feet pe second } \end{gathered}[/tex]The average rate of change is equal to 2 feet per second
To make an open box from a 175cm by 100cm piece of cardboard, equal-sized squares will be cut from each of the four corners and then the sides will be folded up. What is the approximate volume of the largest possible box that can be made?Group of answer choices:A) 324,146 cm^3B)162,073cm^3C) 251,707cm^3D)189,640cm^3
Answers
Given that dimensions of the piece of cardboard are:
[tex]\begin{gathered} l=175\text{ }cm \\ w=100\text{ }cm \end{gathered}[/tex]Where "l" is the length and "w" is the width, you can determine that it has the shape of a rectangle.
You know that equal-sized squares will be cut from each of the four corners and then the sides will be folded up. Then, you can make the following drawing:
By definition, the volume of a rectangle is:
[tex]Volume=length\cdot width\cdot height[/tex]In this case, you can set up that:
[tex]\begin{gathered} length=175-2x \\ width=100-2x \\ height=x \end{gathered}[/tex]Therefore, you can write this equation:
[tex]V=(175-2x)(100-2x)(x)[/tex]Expand it:
[tex]V=(175-2x)(100x-2x^2)[/tex][tex]V=(175)(100x)-(175)(2x)-(2x)(100x+(2x)(2x^2)[/tex][tex]V=4x^3-550x^2+17500x[/tex]Now you need to derivate it using the Power Derivative Rule:
[tex]\frac{d}{dx}(x^n)=nx^{n-1}[/tex]Then:
[tex]V^{\prime}=(4)(3)x^2-(550)(2)x+17500[/tex][tex]V^{\prime}=12x^2-1100x+17500[/tex]Make the equation equal to zero and sove for "x":
[tex]12x^2-1100x+17500=0[/tex]Use the Quadratic Formula:
[tex]x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}[/tex]Substituting:
[tex]\begin{gathered} a=12 \\ b=-1100 \\ c=17500 \end{gathered}[/tex]You get:
[tex]\begin{gathered} x_1\approx20.49 \\ x_2\approx71.18 \end{gathered}[/tex]Therefore, you can make the following Sign Chart:
Then, you can substitute these:
[tex]\begin{gathered} x=20 \\ x=50 \\ x=72 \end{gathered}[/tex]Into the factorize form of the derivated function:
[tex]V=(x+\frac{275-25\sqrt{37}}{6})(x-\frac{275+25\sqrt{37}}{6})[/tex][tex]V=(x+\frac{275-25\sqrt{37}}{6})(x-\frac{275+25\sqrt{37}}{6})[/tex]Please help. I don't really understand monomials and negative exponets
Answers
The standard form of the monomial expression is -1x¹⁰
Monomial expression:
A monomial is an algebraic expression with a single term but can have multiple variables and a higher degree too.
Given,
Here we have the expression
(-2x³)².(-1/4 x⁴)
Now, we have to convert the expression into standard form.
To convert the expression into standard monomial form,
First we have to expand the terms, then we get,
=> (-2²x⁶).(-1/4x⁴)
Then we have to divide the variables and constants separately.
=> (4 x -1/4).(x⁶⁺⁴)
=> -1 . x¹⁰
=> -1x¹⁰
To know more about Monomial expression here.
https://brainly.com/question/28924388
#SPJ1
Convert the polar equation r=3 to a Cartesian equation.x^2+y^2=√3x^2+y^2=3x^2+y^2=9
Answers
For the given equation:
[tex]\begin{gathered} \text{Polar form: } \\ r=3 \\ \\ \text{Cartesian form:} \\ x^2+y^2=3^2 \\ x^2+y^2=9 \end{gathered}[/tex]A tank in the shape of a hemisphere has a diameter of 10 feet. If the liquid that fills the tank has a density of 74.4 pounds per cubic foot, what is the total weight of the liquid in the tank, to the nearest full pound?
Answers
Step 1
State the volume of a hemisphere.
[tex]v=\frac{2}{3}\pi r^3[/tex]Where;
[tex]\begin{gathered} r=\frac{diameter}{2}=\frac{10}{2}=5ft \\ \end{gathered}[/tex]Step 2
Find the volume of the hemisphere
[tex]v=\frac{2}{3}\times\pi\times5^3=\frac{250\pi}{3}ft^3[/tex]Step 3
Find the total weight of the liquid in the tank
[tex]\begin{gathered} \text{Density}=\frac{mass}{\text{volume}} \\ 74.4=\frac{mass}{\frac{250\pi}{3}} \\ \text{mass}=19477.87445lb \\ \text{mass}\approx19478lb \end{gathered}[/tex]Hence the total weight of the liquid in the tank to the nearest full pound = 19478lb
Michael studied the feather lengths of some adult fox sparrows.How long is the shortest feather in the data set?
Answers
From the data set given, 3/4 is the length of the shortest feather of fox sparrow.
Given,
The image is attached with this.
The length of fox sparrow feathers studied by Michael.
1 sparrow with 3/4 inches of feather4 sparrows with 2 inches of feather7 sparrows with 2 1/4 inches of feather5 sparrows with 2 1/2 inches of feather3 sparrows with 2 3/4 inches of feather.We have to find the shortest feather in the data set.
Here,
3/4 inches is the shortest feather and only 1 sparrow has the shortest feather.
2 3/4 inches is the longest feather and 3 sparrows have the longest feather.
That is,
From the data set given, 3/4 is the length of the shortest feather of fox sparrow.
Learn more about length of feather here;
https://brainly.com/question/23986067
#SPJ1
3(2x+4) - 2(4x-1)=20A. x=5B. x=-5C. x=3D. x=-3
Answers
we have the following:
[tex]3(2x+4)-2\left(4x-1\right)=20[/tex]solving for x:
[tex]\begin{gathered} 3(2x+4)-2\left(4x-1\right)=20 \\ 6x+12-8x+2=20 \\ -2x=20-12-2 \\ -2x=6 \\ x=\frac{6}{-2} \\ x=-3 \end{gathered}[/tex]The answer is x = -3
I need help with review on functions
Answers
The answer is Option 2
Its not a function
The domain and range of the function is shown at the various endpoints of the graph.
At every point you can always identify a value for x (the input value) and also a corresponding value for y (the output value).
Please note the endpoints marked in blue.
These are the endpoints, and for every point, you will have (x, y).
However, note that at the endpoints, the values of y remains the same.
For every relation to be a function, there must be exactly one corresponding y value for every x value. As shown by the blue markings on the graph, the x values on the horizontal axis both have the same y value (which is zero).
Hence, the relationship shown by the graph is not a function
graph the function y=sqrt(x+6)+2. which point lies on the graph
Answers
Explanation
We are given the following function:
[tex]y=\sqrt{x+6}+2[/tex]We are required to graph the function.
Using a graphing calculator, we have:
Hence, the answer is (-2, 4).
The last option is correct.
The function table below is intended to represent the relationship y=-5x+1. However, one of the entries for y does not correctly fit the relationship with x.
Answers
Answer:
Step-by-step explanation:
none of the answers are correct
Solve the equation. Check your solution.20x - 4= 50x + 2x=(Simplify your answer. Type an integer or a simplified fraction.)
Answers
20x - 4 = 50x + 2
Solve for x
20x - 50x =
2x + 4x = 3x + 3x Solve for x.
Answers
You have the following expression:
2x +4x = 3x + 3x
in order to solve for x, proceed as follow:
2x +4x = 3x + 3x simplify like terms both sides
6x = 6x
Due to the previous result is the trivial solution, it means that the equation has infinite solutions.
How do I do this, I’m unsure how to go about it
Answers
Given:
[tex]\sqrt{\frac{6}{x}}\cdot\sqrt{\frac{x^2}{24}}[/tex]Simplify:
[tex]=\sqrt{\frac{6}{x}}\cdot\frac{\sqrt{x^2}}{\sqrt{24}}=\sqrt{\frac{6}{x}}\cdot\frac{x}{2\sqrt{6}}[/tex]Apply the properties of fractions:
[tex]=\frac{\sqrt{\frac{6}{x}}x}{2\sqrt{6}}[/tex]Simplify:
[tex]=\frac{\frac{\sqrt{6}}{\sqrt{x}}x}{2\sqrt{6}}=\frac{\sqrt{6}\sqrt{x}}{2\sqrt{6}}[/tex]Eliminate common terms:
[tex]=\frac{\sqrt{x}}{2}[/tex]Answer:
[tex]\frac{\sqrt{x}}{2}[/tex]Convert decimal to 0.147 to fraction ( the last digit 7 repeating)
Answers
Answer:
133/900
Explanation:
To convert the decimal 0.147777 to a fraction, we first identify the decimal part, so we have 147 as a decimal part.
Then, we subtract 14 because that part is not repeating. So:
147 - 14 = 133
Now, we need to divide by 9 to get the repeating part, but the repeating part starts at the third decimal place, so we will divide by 900 instead of 9.
Therefore, 0.147777... as a decimal is:
[tex]0.14777\ldots=\frac{133}{900}[/tex]So, the answer is 133/900
It's a gross thought, but the number (N) of bacteria in refrigerated food is given by latex- 1≤T≤20 where T is the temperature of the food in degrees Celsius. When you take the food out of the refrigerator, the temperature of the food is given by T(t)=3t+2, 0≤t≤6 where t is the time in hours. Find the composition N(T(t)) and interpret what it means in this context.
Answers
Given that the concentration of bacteria in the refrigerated food is
[tex]10T^2-20T-6----\mleft\lbrace1\mright\rbrace[/tex]and the temperature of the food is given by
[tex]T(t)=3t+2-----\mleft\lbrace2\mright\rbrace[/tex]Therefore, N(T(t) is given by
[tex]N\mleft(T(t)\mright)=10(3t+2)^2-20(3t+2)^{}-6[/tex]Then,
[tex]\begin{gathered} N(T(t))=10(3t+2)^2-20(3t+2)^{}-6 \\ =10(9t^2+6t+6t+4)-60t-40-6 \\ =10(9t^2+12t+4)-60t-46 \\ =90t^2+120t+40-60t-46 \\ =90t^2+60t-6 \end{gathered}[/tex]Answer: The composition is
[tex]N(T(t))=90t^2+60t-6[/tex]It can be interpreted as the concentration of bacteria in the food when outside of the refrigerator with time.
I need help with my question
Answers
The opposite of a number is the same as multiplying it by -1. any negative number, it's opposite is that same number positive. And any positive number is that same number negative.
Our number W is 5. Then, the opposite number is - 5.
To draw a point at - 5 from 5, we just need to move the difference between them to the left. The difference between 5 and -5 is given by
[tex]|5-(-5)|=|5+5|=|10|=10[/tex]Then, to draw point V we need to move 10 units to the left of Point W.
Evaluate the expression [tex]9 + 7 - 3 \times 3 - 2[/tex]
Answers
I need help answering the 2nd part of this question
Answers
An identity function has one output value for each input value.
G is an identity function.
To find its equation apply the slope-intercept form:
y=mx +b
Where:
m= slope ( rise / run)
b= y-intercept ( where the function crosses the y axis)
By looking at the graph we can see that it crosses (0,0) so, b= 0.
And for every unit to right along the x-axis, it goes up by 1 unit along the y axis.
So, m= 1/1 = 1
Equation:
y = x
Sean, Kevin and Bill take classes at both JJC and CSU. Sean takes 8 credits at JJC and 4 credits at CSU; Kevin takes 10 credits at JJC and 6 at CSU: Bill takes 6 credits at JJC and 4 at CSU; the cost per credit at JJC is $103 and at CSU is $249. a) Write a matrix A that gives the credits each student is taking and B that gives the cost per credit at each school. b) Find the dimension of A and B. c) Find the product AB and the names of its rows and columns.
Answers
ANSWER:
a)
[tex]\begin{gathered} A=\begin{pmatrix}8 & 4 \\ 10 & 6 \\ 6 & 4\end{pmatrix} \\ B=\begin{pmatrix}103 \\ 249\end{pmatrix} \end{gathered}[/tex]b)
Dimension A = 3 x 2
Dimension B = 2 x 1
c)
Cost of credits
Sean $1820
Kevin $2524
Bill $1614
[tex]\begin{pmatrix}Sean \\ \: Kevin \\ \: Bill\end{pmatrix}\begin{pmatrix}1820 \\ \: 2524 \\ \: 1614\end{pmatrix}[/tex]STEP-BY-STEP EXPLANATION:
With the help of the statement, we create the matrices A and B:
[tex]\begin{gathered} A=\begin{pmatrix}8 & 4 \\ 10 & 6 \\ 6 & 4\end{pmatrix}\rightarrow3\times2 \\ B=\begin{pmatrix}103 \\ 249\end{pmatrix}\rightarrow2\times1 \end{gathered}[/tex]Now, we calculate the product just like this:
[tex]\begin{gathered} \text{Product }A\cdot B=\begin{pmatrix}8\cdot103+4\cdot249 \\ 10\cdot103+6\cdot249 \\ 6\cdot103+4\cdot249\end{pmatrix}=\begin{pmatrix}1820 \\ \: 2524 \\ \: 1614\end{pmatrix} \\ \text{Product }A\cdot B=\begin{pmatrix}Sean \\ Kevin \\ Bill\end{pmatrix}\begin{pmatrix}1820 \\ 2524 \\ 1614\end{pmatrix} \end{gathered}[/tex]Suppose you have a piece of ribbon that is 6 feet long, and you cut off one piece that's 3 2/3
inches long and a second piece that's 2 5/6 inches long. How much ribbon is left in inches?
inches of ribbon left
Answers
Answer:
65 1/2 inches of ribbon is left, my exact work is shown on a piece of paper below if you need it.
Step-by-step explanation:
1 foot = 12 inches
6 x 12 = 72 inches
72 - (3 2/3 + 2 5/6) = ?
My explanation:
The rib ion originally started at 6 feet
You first cut 3 2/3 off, so your now left with 7/3 or 2 1/3 (simplified)
Now your left with 2 1/3.
Then you cut a second piece off, 2 5/6 inches….so 2 5/6 minus 2 1/3 = 1/2
So you should have about 1/2 of a ribbon left.
(I tried btw. I’m very sleepy rn.)
Kristy downloads two songs to her MP3 player. The songs are 3 1/10 minutes and 4 2/3 minutes long. About how many minutes of memory will these two songs use altogether?
Answers
We have:
Song 1 = 3 1/10 minutes
Song 2 = 4 2/3 minutes
Minutes of memory of two songs:
[tex]3\frac{1}{10}+4\frac{2}{3}=\frac{31}{10}+\frac{14}{3}=\frac{3\times31+10\times14}{30}=\frac{93+140}{30}=\frac{233}{30}=7\frac{23}{30}[/tex]Answer:
[tex]7\frac{23}{30}\text{ minutes}[/tex]Lines AD and BC are parallel. What is the angle measurement of Angle DAE(Point A)?D150°45°BсFYour answer
Answers
Solution
For this case we can find the angle:
m < ECB = 30º
And we can find the angle CEB and we got:
m < CEB = 180 -30 - 45 = 105
And then the angle DAE would be:
m < DAE = 30º
John has two apples, he gives Jane 251. How many apples does John have? Please help 2nd grade is so hard.
Answers
a point is chosen at random in the large square. find the probability that the point is in the smaller shaded square. each side of the large square: 16 cmeach side of the shaded square: 6 cm*round to the nearest hundredth
Answers
The Probability of the point being in the smaller shaded square is 0.79.
What is meant by probability?Probability equals possibility. It is a branch of mathematics concerned with the occurrence of a random event. The value ranges from 0 to 1. Probability has been introduced in mathematics to predict how likely events are to occur.Probability = the number of possible outcomes. the total number of possible outcomes For example, the probability of flipping a coin and getting heads is 12, because there is only one way to get a head and the total number of possible outcomes is two (a head or tail).The probability is a measure of the likelihood of an event occurring. It assesses the event's likelihood. P(E) = Number of Favorable Outcomes/Number of Total Outcomes is the probability formula.Therefore,
|Ω| = 6² = 36
< br / > |A| = 3.14.3² = 278.26
Then we get,
< br / > P |A| = 28.26/36 ≈ 0.79
∴ the probability that the point is in the smaller shaded square is 0.79
To learn more about probability, refer to:
https://brainly.com/question/25870256
#SPJ1
The crew knows the amount of dirt the truck can hold each trip in cubic yards.
Answers
Given:
Measurements of hole are 48ft 39ft and and 9ft
Required:
Volume in cubic yd
total number of trip
total cost of trip
Explanation:
First we need to convert given measurements from ft to yd
[tex]\begin{gathered} 3ft=1yd \\ 48ft=16yd \\ 39ft=13yd \\ 9ft=3yd \end{gathered}[/tex]
A)
[tex]V=lhw=16*13*3=624yd^3[/tex]B)
11 cubic yd in 1 trip
then
624 cubic yd in x trip
[tex]x=\frac{624}{11}=56.7\approx57[/tex]C)
cost for 1 trip is $1175
then
cost for 57 trip is y
[tex]y=57*1175=66975[/tex]Final answer:
Volume in cubic yd is 624
total number of trips is 57
total cost of trip $66975
54 is 120 percent of what number ?
Answers
Answer:
120% of 54 =
120% × 54 =
120/100 × 54 =
(120 ÷ 100) × 54 =
120 × 54 ÷ 100 =
6,480 ÷ 100 =
64.8
Percentage of 120% of 54
120% of 54 = 64.8
and to prove that we got the right answer do what we did above in reverse below
64.8 ÷ 54 =
1.2 =
1.2 × 100/100 =
(1.2 × 100)/100 =
120/100 =
120%
Step-by-step explanation:
there are 5 adult cats, 6 middle aged cats, and ___ kittens, if there are 19 animals in total, how many kittens are there, solve for the blank.
Answers
ANSWER
There are 8 kittens
EXPLANATION
If the sum of the number of adult cats, middle aged cats and kittens is 19:
[tex]\begin{gathered} \text{adult}+\text{middle aged+kittens=19} \\ 5+6+\text{kittens}=19 \\ \text{kittens}=19-5-6 \\ \text{kittens}=8 \end{gathered}[/tex]in slope intercept form what is the line perpendicular to y=2x -5 that passes through the (2, -5) point
Answers
The most appropriate choice for equation of line in slope intercept form will be given by-
[tex]y = -\frac{1}{2}x - 4[/tex] is the required equation of line
What is equation of line in slope intercept form?
The most general form of equation of line in slope intercept form is given by y = mx + c
Where m is the slope of the line and c is the y intercept of the line.
Slope of a line is the tangent of the angle that the line makes with the positive direction of x axis.
If [tex]\theta[/tex] is the angle that the line makes with the positive direction of x axis, then slope (m) is given by
m = [tex]tan\theta[/tex]
The distance from the origin to the point where the line cuts the x axis is the x intercept of the line.
The distance from the origin to the point where the line cuts the y axis is the y intercept of the line.
Here,
The given equation of line is y = 2x-5
Slope of this line = 2
Slope of the line perpendicular to this line = [tex]-\frac{1}{2}[/tex]
The line passes through (2 , -5)
Equation of the required line = [tex]y - (-5) = \frac{1}{2}(x - 2)[/tex]
[tex]y +5=-\frac{1}{2}x+1\\y = -\frac{1}{2}x +1 -5\\y = -\frac{1}{2}x -4[/tex]
To learn more about equation of line in slope intercept form, refer to the link-
brainly.com/question/25514153
#SPJ9
The figure on the right is a scale drawing of the figure on the left. What is the scale factor?
Answers
In order to find the scale factor, we just need to divide one side of the right figure by the corresponding side in the left figure.
So, taking the sides SU and PR, we have:
[tex]\text{scale}=\frac{SU}{PR}=\frac{12}{8}=1.5[/tex]So the scale factor is 1.5.