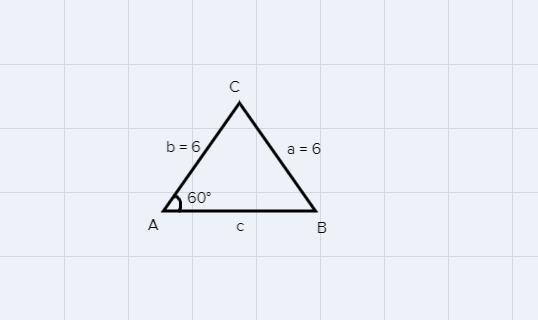
Complete a triangulation calculation to measure the distance between actual objects in or near your home. include a well-labeled diagram.
Answers
Triangulation means the measuring of distances in surveys with triangles. If the distance of two objects and the angle between is knwon, the distance between these objects can be calculated.
Given the diagram we have:
So, the distance between both objects will be calculated by:
[tex]c=\sqrt{a^2+b^2-2ab\cdot\cos\theta}[/tex]Where:
Distance to the first object a = 6
Distance to the first object b = 6
Angle between both objects θ = 60°
Substitute the values, we have:
[tex]c=\sqrt{6^2+6^2-2(6)(6)\cdot\cos60}[/tex]Simplify:
[tex]c=\sqrt{36+36-72(0.5)}=\sqrt{72-36}=\sqrt{36}=6[/tex]So, the distance between both objects c = 6 inches
Related Questions
Ava borrowed some money from her friend in order to help buy a new video game system. Ava agreed to pay back her friend $2 per week, and after 5 weeks, Ava still owed her friend $10. Write an equation for L, in terms of t, representing the amount Ava owes her friend after t weeks.
Answers
We know that Ava is paying $2 dollars per week so if L is the money that she owes and t is the number of weeks, and I is the initial debt so we can write an equation like:
[tex]L=I-2t[/tex]Now we can replace the info we have to find the value of I so:
[tex]10=I-2(5)[/tex]and we solve for I
[tex]\begin{gathered} I=10+10 \\ I=20 \end{gathered}[/tex]So the final equation will be:
[tex]L=20-2t[/tex]The lengths of two sides of an isosceles triangle are 8 and 10. The length of the third side could beA. either 8 or 10B. 6, onlyC. 8, onlyD. 10, only
Answers
From Triangle Inequality Theorem
The sum of any 2 sides of a triangle must be greater than the measure of the third side.
The sum of 2 sides is less than (or equal to) the measure of a third side.
In an isosceles triangle, two sides are equal.
Then we have an option the third side= 8. Let's analyze!
c+a> b - for a and c =8
8+8 > 10
16> 10
The second option is the third side= 10. Let's analyze!
c+a> b - for a and c =10
10+10> 8
20> 8
Answer
A. either 8 or 10
An old blackboard needs to be covered with cork. The picture shows the size of the blackboard. 40 in. 60 in. What is the area to be covered? A 100 in? B 200 in? C 1200 in 2 D2,400 in2
Answers
In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
area = ?
Step 02:
WITHOUT using a graphing device, find the x- and y-intercepts of the graph:y = 3x^3 - 9x^2
Answers
Given:
The function is,
[tex]y=3x^3-9x^2[/tex]To find the x intercept set y=0,
[tex]\begin{gathered} y=3x^3-9x^2 \\ 3x^3-9x^2=0 \\ x^2(3x-9)=0 \\ \Rightarrow x^2=0,3x-9=0 \\ x=0,3x=9 \\ x=0,x=\frac{9}{3} \\ x=0,x=3 \end{gathered}[/tex]So, x-intercepts are ( 0 , 0 ), ( 3, 0 ).
Now to find y-intercepts set x=0.
[tex]\begin{gathered} y=3x^3-9x^2 \\ y=3(0)-9(0) \\ y=0 \end{gathered}[/tex]y- intercept is ( 0 ,0 )
Answer: option e)
Let p be "x+4=13" and q be "x=9." Which of the following statements is a biconditional?Select the correct answer below:x+4=13 and x=9.If x+4=13, then x=9.x+4=13 if and only if x=9.x+4=13 only if x=9.
Answers
For two given simple statements P and Q, if they are connected with the logical connectivity 'if and only if', then the compund statement is called biconditional statement.
Now,
P: x+4=13
q: x=9
Then, their biconditional statement is x+4=13 if an donly if x=9
Hence the correct answer is (c)
The solution to the equation4(x + 2) =3(5-x) is:
Answers
ANSWER:
The value of x is 1, that is, the solution of the equation is 1
STEP-BY-STEP EXPLANATION:
We have the following equation:
[tex]4\cdot(x+2)=3\cdot(5-x)[/tex]Solving for x:
[tex]\begin{gathered} 4x+8=15-3x \\ 4x+3x=15-8 \\ 7x=7 \\ x=\frac{7}{7} \\ x=1 \end{gathered}[/tex]Question 10
Answer:
Not yet answered Marked out of 2.00
A tyre made of rubber (density 1.2 g/cm³) has a mass of 3.6 kg.
Find its volume.
(Use ^sign from the computer's keyboard to express the power of the units for the volume
Question 11
Not yet answered Marked out of 1.00
Flag question
What percentage of the grid is shaded?
PFlag question
Answers
1.volume = mass*density
v = 1.2 * 3.6 = 4.32 cm3
The density of a substance quantifies how tightly its molecules are packed, which affects how heavy or light it is.
Density is calculated as follows: density=mass/volume. Most often, mass is measured in grams or kilograms. Most often, volume is measured in cubic centimeters (cm3), cubic meters (m3), or millileters (mL).
How can you find mass from density?
multiply the volume by the density.
Mass per unit volume is the definition of density.
ρ = m V
This can be rearranged to yield the mass expression.
m = ρ × V
Example:
What mass of the liquid is present if 500 mL of it has a density of 1.11 g/mL
m = ρ × V = 500 mL × 1.11 g
1 mL = 555 g
to learn more about density=mass/volume refer to:
https://brainly.com/question/952755
#SPJ13
What is the value of 0 put a comma and space between answer sin61°=cos=0; cos17°=sin0;
Answers
For
[tex]\begin{gathered} \sin 61=\cos \theta \\ \theta=\cos ^{-1}(\sin 61) \\ \end{gathered}[/tex]For
[tex]\begin{gathered} \cos 17=\sin \theta \\ \theta=\sin ^{-1}(\cos 17) \\ \end{gathered}[/tex]how do you simplify this expression to become x ^3 -8
Answers
we have the expression
[tex]\begin{gathered} (x^3-4)-4 \\ remove\text{ the parenthesis} \\ x^3-4-4 \\ combine\text{ like terms} \\ x^3-8 \end{gathered}[/tex]Instructions: Find the value of that completes the square and creates a perfect square trinomial.
Answers
Solution:
Given the expression;
[tex]x^2+18x+c[/tex]c is the half of square of coefficient of x. That is;
[tex]\begin{gathered} x^2+18x+c=x^2+18x+(\frac{1}{2}(18))^2 \\ \\ x^2+18x+c=x^2+18x+9^2 \\ \\ x^2+18x+c=x^2+18x+81 \\ \\ x^2+18x+81=(x+9)(x+9) \end{gathered}[/tex]Hence, the value of c is;
[tex]c=81[/tex]Review the proof. Which step contains an error? step 2 step 4step 6step 8
Answers
Answer
Option C is correct.
Step 6 contains the error.
Explanation
Looking through the steps, we can see easily that the mistake occurs at the 6th step, specifically when the process moves from step 5 to step 6
-1 + cos θ = -2 sin² (θ/2)
If one multiplies through by -1
1 - cos θ = 2 sin² (θ/2)
NOT 1 + cos θ = 2 sin² (θ/2)
Hope this Helps!!!
On a number line, let point P represent the largest integer value that is less than V380.Let point Q represent the largest integer value less than 54.What is the distance between P and Q?A. 10B. 11C. 12D. 13
Answers
We have to find P and Q first.
P is the largest integer that is less than the square root of 380.
P is 19.
Q is the largest number that is less than the square of 54.
Q is 7.
Then the distance between P and Q is |19-7|=12.
Answer: C. 12
if the equation, in which n, m, and r are constants, is true for all positive values of a, b, and c, what is the value of n?
Answers
since n, mand r are the constants for a, b,c n=6
which equation represents a line having a slope of 5/2 and a y intercept of (0,-4)
Answers
First you must know the standard equation of a line and this is expressed as:
[tex]y\text{ = mx+c}[/tex]where:
m is the slope of the line
c is the intercept
Given
Slope m = 5/2
Next is to get the intercept c:
To do that, you will substitute m = 5/2 and the coordinate (0, -4) into the equation above as shown:
[tex]\begin{gathered} -4\text{ = 5/2(0)+c} \\ -4\text{ = 0+c} \\ c\text{ = -4} \end{gathered}[/tex]Next is to get the required equation by substituting m = 5/2 and c = -4 into the equation above as shown:
[tex]\begin{gathered} y\text{ = mx + c} \\ y\text{ = }\frac{5}{2}x\text{ +(-4)} \\ y\text{ = }\frac{5}{2}x\text{ - 4} \end{gathered}[/tex]Hence the required equation is espressed as:
[tex]y\text{ = }\frac{5}{2}x-4[/tex]In AOPQ, 0 = 500 cm, p = 600 cm and q=380 cm. Find the measure of P to thenearest 10th of a degree.
Answers
Answer: Triangle has three sides, which are:
[tex]\begin{gathered} O=500\operatorname{cm} \\ P=600\operatorname{cm} \\ Q=380\operatorname{cm} \\ \end{gathered}[/tex]We need to find the angle p, that is right across the side P:
[tex]\angle A=\arccos (\frac{b^2+c^2+a^2}{2bc})=0.97895\text{rad}=56.09\text{degres}[/tex]This is the value of angle A
Suzy has $2000 to invest and needs $2400 in 12 years. What annualrate of return will she need to get in order to accomplish her goal, if theinterest is compounded continuously? (Round your answer to twodecimal places) A = Pert
Answers
Given data:
Principal Amount=$2000.
Final Amount=$2400
Time period(t)=12 years
Let the rate of return be r.
As per formula of continous compunding:
[tex]\begin{gathered} \text{Final amount=Principal}(e^{rt}) \\ 2400=2000(e^{12r}) \\ e^{12r}=\frac{2400}{2000} \\ e^{12r}=1.2 \\ 12r=\ln (1.2) \\ 12r=0.1823 \\ r=0.01519 \end{gathered}[/tex]Thus, the rate of interest required is 1.519%.
you are standing 200 feet from a tall building . The angle from your feet to the top of the building is 51°.
Answers
the sum of angles in a triangle is 180
missing angle + 90 + 51 = 180
missing angle = 180 - 141
missing angle = 39 degrees.
in the triangle,
[tex]\frac{x}{200}=\tan 51[/tex]x = 200 tan51
x = 200 * 1.234
x = 246.97 ft apporx 247 ft
'so the length x = 247 ft
that is greater than 200
so the answer is
x > 200 ft
I dont want you to answer question for me, i have already answered it as shown in the picture. I want you to let me know if i have provided an answer worth full marks and if not tell me how i could improve it
Answers
Answer:
[tex]\begin{equation} \sqrt{3}-1,2 \sqrt{10} \div 5, \sqrt{14}, 3 \sqrt{2}, \sqrt{19}+1,6 \end{equation}[/tex]Explanation:
Given the irrational numbers:
[tex]$3 \sqrt{2}, \sqrt{3}-1, \sqrt{19}+1,6$, $2 \sqrt{10} \div 5,\sqrt{14}$[/tex]In order to arrange the numbers from the least to the greatest, we convert each number into its decimal equivalent.
[tex]\begin{gathered} 3\sqrt{2}=3\times1.414\approx4.242 \\ \sqrt{3}-1\approx1.732-1=0.732 \\ \sqrt{19}+1\approx4.3589+1=5.3589 \\ 6=6 \\ 2\sqrt{10}\div5=2(3.1623)\div5=1.2649 \\ \sqrt{14}=3.7147 \end{gathered}[/tex]Finally, sort these numbers in ascending order..
[tex]\begin{gathered} \sqrt{3}-1\approx1.732-1=0.732 \\ 2\sqrt{10}\div5=2(3.1623)\div5=1.2649 \\ \sqrt{14}=3.7147 \\ 3\sqrt{2}=3\times1.414\approx4.242 \\ \sqrt{19}+1\approx4.3589+1=5.3589 \\ 6=6 \end{gathered}[/tex]The given numbers in ascending order is:
[tex]\begin{equation} \sqrt{3}-1,2 \sqrt{10} \div 5, \sqrt{14}, 3 \sqrt{2}, \sqrt{19}+1,6 \end{equation}[/tex]Note: In your solution, you can make the conversion of each irrational begin on a new line.
Enzo counted the number of sunny days each of his favorite towns had in the year 2013 and graphed theresults.Light LandBright VillagePlaceShiny TownSun City -050100150200250300Number of Sunny Days
Answers
From the graph, we can see that the town that had most sunny days was Shiny Twon.
So, between this town and Sun City, we have Bright Viallge, that had a number of sunny days between Sun City and Shiny Town.
So the answer is Bright Village.
1. Beyonce went to the mall and saw a massage chair that she would have to take a loan out for $6,500 to purchase. The bank said that she could get a simple interest rate of 8% for 5 years. What is the TOTAL amount that Beyonce will pay for the chair? * O $2,600 $910 O $9,100 O $260
Answers
The simple interest formula is:
[tex]i=\text{Prt}[/tex]Where
i is the interest earned
P is the initial (loan) amount
r is the rate of interest
t is the time
Given,
P = 6500
r = 8%, or, 8/100 = 0.08
t = 5
Substituting, we get:
[tex]\begin{gathered} i=\text{Prt} \\ i=6500\times0.08\times5 \\ i=2600 \end{gathered}[/tex]This is only the interest. Beyonce would need to pay the original (6500) plus this interest (2600) in total. Thus, she will have to pay:
[tex]6500+2600=9100[/tex]5+3x=5x-19 I need help solving Multi Step Equations with Variables on both sides.
Answers
The equation we have is:
[tex]5+3x=5x-19[/tex]when we have the variable on both sides of the equation, what we need to do is move all of the variables to one side of the equation.
For example, in this case, to have all of the variables on the same side, we substract 5x to both sides:
[tex]5+3x-5x=5x-19-5x[/tex]On the right side 5x and -5x cancel each other, and we are left with:
[tex]5+3x-5x=-19[/tex]Next, we add the like terms on the left side, 3x-5x is equal to -2x:
[tex]5-2x=-19[/tex]Since we need to solve for x, we substract 5 to both sides, to leave the variable term alone:
[tex]-2x=-19-5[/tex][tex]-2x=-24[/tex]And finally, we divide both sides by -2:
[tex]\begin{gathered} -\frac{2x}{-2}=\frac{-24}{-2} \\ \\ x=12 \end{gathered}[/tex]Answer: x=12
12. Consider the figure shown.11CDBWhat does ACB represent?A. a rayB an oroc. an angloDa lino sogmont
Answers
Take into account that ACB is an angle, because you can measure the vertex ACB just as an angle.
Then, the answer is:
ACB
Personal Math Trainer Lesson 15.2 - Homework - Homework 112131415 5 16 17 8 Margo can purchase tile at a store for $0.69 per tile and rent a tile saw for $56. At another store she can borrow the tile saw for free if she buys tiles there for $1.39 per tile. How many tiles must she buy for the cost to be the same at both stores? Margo must buy tiles for the cost to be the same at both stores.
Answers
Let Margo buy x number of tiles, So total cost of tiles and tile saw at first store is,
[tex]y=0.69x+56[/tex]The total cost equation for tile and tile saw for second store (which provide tile saw for free).
[tex]\begin{gathered} y=1.39x+0 \\ =1.39x \end{gathered}[/tex]Determine the number of tiles for total cost of tiles and tile saw to be equal from both store is,
[tex]\begin{gathered} 1.39x+0.69x+56 \\ 1.39x-0.69x=56 \\ 0.70x=56 \\ x=\frac{56}{0.70} \\ =80 \end{gathered}[/tex]So Margo purchase 80 tiles, such that total cost is equal from both the stores.
What is the explicit rule for the nth term of the geometric sequence? Thanks
Answers
Solution.
Given the sequence
[tex]3,18,108,648,3888[/tex]Test which kind of sequence it is
[tex]\begin{gathered} \frac{18}{3}=6 \\ \frac{108}{18}=6 \\ The\text{ sequence has a common ratio which is 6. } \\ Thus,\text{ it is a geometric sequence} \\ \end{gathered}[/tex][tex]\begin{gathered} The\text{ nth term of a geometric sequence can be determined by the formula} \\ a_n=ar^{n-1} \\ where\text{ a = 1st term} \\ r=common\text{ ratio} \end{gathered}[/tex][tex]a_n=3(6^{n-1})[/tex][tex]The\text{ answer is a}_n=3(6^{n-1})[/tex]A landscaper has built a U-shaped raised bed in a vegetable garden as shown in the figure. How many cubic yards of soil should be ordered to fill the bed to a depth of 30 inches?
Answers
First calculate the area of the shaded region by considering the U-shaped bed as formed by three rectangles, as follow:
where the lengths of the sides of the rectangles corresponds with the dimensions of the U-shaped bed.
Then, for the area of the figure, use the formula for the area of a rectangle, for all three rectangles, as follow:
A = 5*18 + 3*20 + 5*18
A = 90 + 60 + 90
A = 240
Then, the area is 240 in^2
Next, convert the previous result to yd^2. Use the equivalence 1 yd = 36 in:
[tex]240in^2\cdot\frac{(1yd)^2}{(36in)^2}=0.185yd^2[/tex]Now, to find the volume convert 30 in to yards:
[tex]30in\cdot\frac{1yd}{36in}=0.83yd[/tex]Finally, multiply the previous result by the area of the figure:
[tex]0.185yd^2\cdot0.83yd=0.154yd^3[/tex]The function h is defiend by the following rule. h(x)=5x+4.
Answers
we have the function
h(x)=5x+4.
Create a table
For x=-4
substitute the value of x in the function to obtain h(x)
so
h(-4)=5(-4)+4
h(-4)=-20+4
h(-4)=-16
For x=-3
h(-3)=5(-3)+4
h(-3)=-15+4
h(-3)=-11
For x=1
h(1)=5(1)+4
h(1)=9
For x=2
h(2)=5(2)+4
h(2)=14
For x=5
h(5)=5(5)+4
h(5)=29
The selling price of a refrigerator, is $537.60. If the markup is 5% of the dealer's cost, what is the dealer's cost of the refrigerator?
Answers
The cost price of dealer is $512.
We have to find the dealer's cost of refrigerator.
We know that mark up is on dealer's cost.
We have been given the markup as 5%
Let the dealer's cost of refrigerator be x,
Now, we know that there is a markup on it
So, we will calculate the marked up price
Marked up price = (Cost price * Markup percent)/100 + cost price
Marked up price = x*5/100 + x
Marked up price = 5x/100 + x
Marked up price = x/20 + x = (x+20x)20
Marked up price = 21x/20
We know that marked up price is the selling price and we have been given the selling price of the refrigerator
537.60 = 21x/20
537.60*20 = 21x
10752 = 21x
x = 10752/21
x = 512
The dealer's cost price is $512.
To know more about mark up price,
https://brainly.com/question/2027650
Select the correct answer.Consider this equation,tan(6)If 8 is an angle in quadrant II, what is the value of cos(8),OA.B._vOD.
Answers
Remember the definition of the tangent function:
[tex]\tan \theta=\frac{\sin \theta}{\cos \theta}[/tex]Then, we notice that:
[tex]\tan (\theta)=-\sqrt[]{\frac{19}{17}=}-\sqrt[]{\frac{\frac{19}{6}}{\frac{6}{17}}}=\frac{\sin \theta}{\cos \theta}[/tex]Then, we can conclude that:
[tex]\frac{\sin \theta}{\cos \theta}=-\frac{\sqrt[]{\frac{19}{6}}}{\sqrt[]{\frac{6}{17}}}[/tex]Something important to remember is that, in quadrant II, the value of sin(x) is positive, whereas the value of cos(x) is negative
So,
[tex]\begin{gathered} \sin (\theta)=\sqrt[]{\frac{19}{6}} \\ \Rightarrow\frac{1}{\cos \theta}=-\frac{1}{\sqrt[]{\frac{6}{17}}} \\ \Rightarrow\cos \theta=-\sqrt[]{\frac{17}{6}} \end{gathered}[/tex]Therefore, the answer to the question is option A
hours worked. pay2. 12.504. 25.006. 37.508. 50.00write a function rule for the table
Answers
The Function is the equation of a line
Step1: we pick any two-point in the of the table and substitute them into the formula below
[tex]\frac{y-y_1}{x-x_1}=\frac{y_2-y_1_{}}{x_2-x_1}[/tex](y - y₁) / (x - x₁) = (y₂ - y₁) / (x₂ - x₁)
Let us pick the point (4,25) and (8,50)
where
[tex]x_1=[/tex]Which of the following are solutions to the inequality below? Select all that apply.
Answers
The first step to solving this problem is to put the variable on one side. Thus, you must move 7 to the right side to make [tex]\frac{f}{25} \leq -3[/tex]
Next, you must multiply the 25 to the right side to isolate the variable
You get [tex]f \leq -75[/tex]
With this explained, the answer would be the second option (f=-75)
Hope this helped :)