Answers
ANSWER
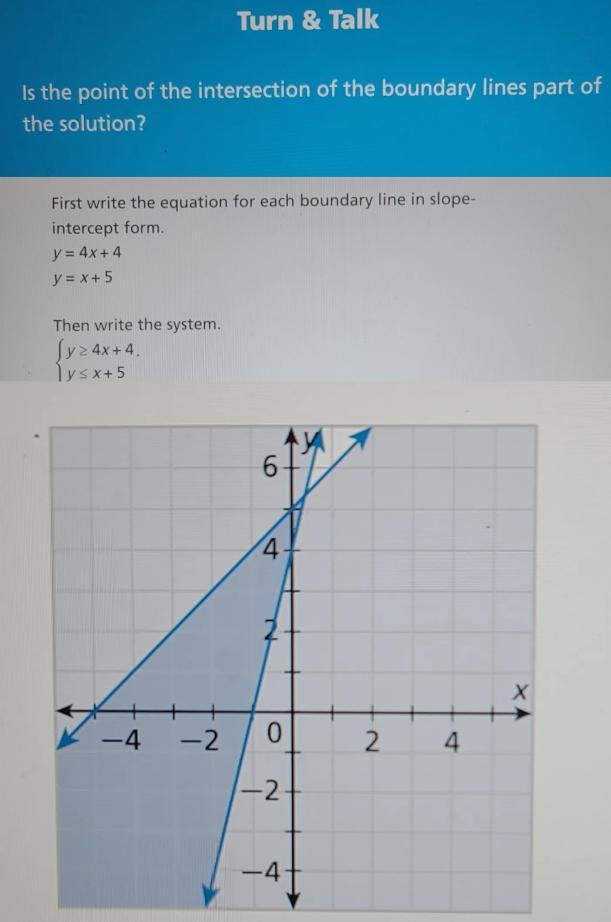
Yes
EXPLANATION
The system of inequalities shows that y is greater than or equal to the first line and less than or equal to the second line. This means that any point on both lines is a solution to the system.
Hence, the intersection of the boundary lines is part of the solution.
Related Questions
Complete the table .....Which parts of the arithmetic sequence in the left of the table match up with the linear function on the right?
Answers
Let's expand the formula for arithmetic sequence.
[tex]\begin{gathered} a_n=a_1+d(n-1) \\ a_n=a_1+dn-d \\ a_n=dn+(a_1-d) \end{gathered}[/tex]The linear function is:
[tex]f(x)=ax+b_{}[/tex]Matching both equations, we can say:
[tex]\begin{gathered} a_n\gg\gg f(x) \\ d\gg\gg a \\ n\gg\gg x \\ a_1-d\gg\gg b \end{gathered}[/tex]On a 7 question multiple-choice test, where each question has 2 answers, what would be the probability of getting at least one question wrong?Give your answer as a fraction
Answers
Solution
- This is a Binomial probability question. The formula for Binomial probability is:
[tex]\begin{gathered} P(r)=\sum\text{ }^nC_rp^rq^{n-r} \\ where, \\ n=The\text{ total number of trials} \\ r=\text{ The number of successful trials\lparen where answer is correct\rparen} \\ p=\text{ The probability of success \lparen The probability of getting a question } \\ right) \end{gathered}[/tex]- We have been given:
[tex]\begin{gathered} n=7 \\ \text{ since there can only be two answers, it means that the} \\ \text{ probability of getting a question correct is:} \\ p=\frac{1}{2} \\ q=1-p=\frac{1}{2} \\ \\ \text{ The probability of getting at least 1 question wrong means the } \\ probability\text{ of getting 1, 2, 3, 4, 5, 6, or 7 question wrong.} \\ \\ \text{ Instead of calculating all these probabilities, we can simply say} \\ P(1)+P(2)+P(3)+P(4)+P(5)+P(6)+P(7)=1-P(0) \end{gathered}[/tex]- Thus, we have:
[tex]\begin{gathered} P(0)=^7C_0(\frac{1}{2})^0(\frac{1}{2})^7 \\ P(0)=\frac{1}{128} \\ \\ 1-P(0)=1-\frac{1}{128}=\frac{127}{128} \end{gathered}[/tex]Final Answer
The answer is
[tex]\frac{127}{128}[/tex]URGENT!! ILL GIVE
BRAINLIEST! AND 100 POINTS
Answers
Answer:
perimeter: add p + m + n
area: use (p × m)/2
find missing side: use p^2 + m^2 = n^2
9. If L 1 equals 120 then what is the measure of its supplement <2=
Answers
Supplementary angles are angles whose addition sums up to 180 degrees.
Therefore, if angle 1 measures 120, then its supplement which is angle 2, must mean both add up to 180.
Hence, you have
Angle 1 + Angle 2 = 180
120 + Angle 2 = 180
Subtract 120 from both sides of the equation
Angle 2 = 180 - 120
Angle 2 = 60 degrees
By definiton, two angles are complimentary angles if they both add up to 90 degrees. Hence if angle L5 equals 50 degrees, then its compliment would be derived as 90 - 50 which equals 40. The compliment of angle L5 which is 50 degrees, equals 40 degrees.
Function g is a transformation of the parent function exponential function. Which statements are true about function g?
Answers
For the given function, The following are true statements:
Four units separate function g from function f.There is a y-intercept for function g. (0,4)Function g has a range of (3,∞ ).Over the range (-, ∞), function g is positive.It may be seen from the graph below that
The g function's graph is 4 units higher than the parent exponential function's graph.
All of the input values for which the function is defined are referred to as the function's domain. The domain of the function is (-, ∞ ) according to the graph of function g.
The location where a function's graph crosses the y-axis is known as the y-intercept. G's graph crosses the y-axis at (0, 4). As a result, the Function g's y-intercept is (0,4).
growing function g across the range (- ∞, 0).
Function output values are referred to as the function's range. It can be seen from the graph that the range of function g is (3, ∞ ).
To learn more about functions, https://brainly.com/question/21145944
#SPJ9
The height of a pole is 15 feet. A line with banners is connected to the top of the poleto a point that is 8 feet from the base of the pole on the ground. How long would theline with banners need to be in order for the pole to be at a 90° angle with the ground?Explain your reasoning.
Answers
In order to have a 90º angle (right angle) the length of the line with banners needs to fullfit the Pythagorean theorem: In a right triangle the squared hypotenuse is equal to the sum of the legs squared:
[tex]h^2=l^2+l^2[/tex]In the given situation the hypotenusa is the line with banners, and the legs are the pole and the 8ft ground from the base of the pole to the end of the line with banners:
h= x
l= 15ft
l= 8ft
[tex]x^2=(15ft)^2+(8ft)^2[/tex]Solve the equation to find the value of x:
[tex]\begin{gathered} x^2=225ft^2+64ft^2 \\ x^2=289ft^2 \\ x=\sqrt[]{289ft^2} \\ x=17ft \end{gathered}[/tex]Then, to make a right triangle the length of the line witg banners need to be 17ftX+87°2x⁰ i have to solve for x it’s a 180 angle HELP ME!!!!!!!!!
Answers
Collect Like terms
X+2x°=180°-87°
3x=93°
Divide both sides by 3 to eliminate the coefficient of “x”
3x/3=93°/3
X=31°
1. what is the area of the board shown on the scale drawing? explain how you found the area.2. how can Adam use the scale factor to find the area of the actual electronics board? remember, he uses a different method than Jason.3. what is the area of the actual electronics board?
Answers
Answer:
1. 1800 square cm.
2. See below
3. 45000 square cm.
Explanation:
Part 1
The dimensions of the drawing are 36cm by 50cm.
[tex]\begin{gathered} \text{The area of the board}=36\times50 \\ =1800\operatorname{cm}^2 \end{gathered}[/tex]Part 2
Given a scale factor, k
If the area of the scale drawing is A; then we can find the area of the actual board by multiplying the area of the scale drawing by the square of k.
Part 3
[tex]\begin{gathered} \text{Area of the scale drawing}=1800\operatorname{cm}^2 \\ \text{Scale Factor,k=5} \end{gathered}[/tex]Therefore, the area of the actual drawing will be:
[tex]\begin{gathered} 1800\times5^2 \\ =45,000\operatorname{cm}^2 \end{gathered}[/tex]helppppppppppppppppppppppppppp
Answers
Step-by-step explanation:
make the fractions decimals and put them on the plot
2000.5 - 351.748 +62.1
Answers
Given the expression :
[tex]2000.5-351.748+62.1[/tex]At first make all the decimal digits equally for all terms
The maximum decimal is 3 so, add 00 to the first and the last terms
So,
[tex]\begin{gathered} 2000.5-351.748+62.1 \\ =2000.500-351.748+62.100 \\ =1710.852 \end{gathered}[/tex]So, the answer is : 1,710.852
Find all solutions of the equation in the interval [0,2pi). csc =7/4 If there is more than one solution, separate them with commas.Do not round any intermediate computations. Give your answer(s) in radians, and round your answer(s) to the nearest hundredth
Answers
Since the cosecant is the inverse of the sine, we can write the following:
[tex]\begin{gathered} \csc (\theta)=\frac{7}{4} \\ \sin (\theta)=\frac{1}{\csc(\theta)}=\frac{1}{\frac{7}{4}}=\frac{4}{7} \end{gathered}[/tex]Then, using a calculator, we can calculate the angle that has a sine of 4/7:
[tex]\begin{gathered} \theta=\sin ^{-1}(\frac{4}{7})_{} \\ \theta=34.85\degree \end{gathered}[/tex]There is one more angle between 0 and 2π that has the same value of 4/7 for the sine, and it's the supplementary angle to the one we found:
[tex]\theta_2=180-\theta_1=180-34.85=145.15\degree[/tex]Therefore the answers are 34.85° and 145.15°.
Converting to radians, we have:
[tex]\begin{gathered} 34.85\cdot\frac{\pi}{180}=0.61 \\ 145.15\cdot\frac{\pi}{180}=2.53 \end{gathered}[/tex]So the final answer is 0.61 and 2.53.
6) Write the equation of the line, in point-slope form, that passes through the point (-2,5) and has a slopeof 3.
Answers
Write the equation of the line, in point-slope form, that passes through the point (-2,5) and has a slope
of 3
___________________________________________________
The point-slope form
y-y1 = m (x-x1)
The slope (m)= 3
The point (x1, y1) = (-2,5)
____________
Replacing
y-5 =3 (x- (-2))
_______________
Answer
(y-5) =3 (x +2)
Do you have any questions regarding the solution?
(2, -3) (4, -2)
Slope intercept
Answers
The slope of the given coordinates is m = 1/2.
What is the slope?A line's steepness can be determined by looking at its slope. The slope is calculated mathematically as "rise over run" (change in y divided by change in x). The slope-intercept form of an equation is used whenever the equation of a line is expressed in the form y = mx + b. M represents the line's slope. B is the b in the point where the y-intercept is located (0, b). For instance, the slope and y-intercept of the equation y = 3x - 7 are 3 and 0, respectively.So, the slope of (2, -3) (4, -2):
The slope formula: m = y₂ - y₁/x₂ - x₁Now, solve for slope by putting the values as follows:
m = y₂ - y₁/x₂ - x₁m = -2 - (-3)/4 - 2m = -2 + 3/2m = 1/2Therefore, the slope of the given coordinates is m = 1/2.
Know more about slopes here:
https://brainly.com/question/3493733
#SPJ13
The correct question is shown below:
Find the slope using the coordinates (2, -3) (4, -2).
Explain how you know 437,160 is greater than 43,716.4 grade student
Answers
437,160 is read as four hundred thirty-seven thousand one hundred sixty and 43,716 is read as fourty-three thousand seven hundred sixteen.
The first number has hundreds of thousand and the second one only has tens of thousand. It means that the first number is greater than the second one.
Another way to know this is because of the number of figures before the decimal point. The first number has 6 figures before the decimal point and the second one only has 5.
That way, we know that 437,160 is greater than 43,716.
Complete the table for y=-3x + 5 and graph the resulting line. -
Answers
We fill the table as follows:
*We assign values for x and solve for y, that is:
*x = 0:
[tex]y=-3(0)+5\Rightarrow y=5[/tex]So, the value of y when x = 0 is 5.
*x = 1:
[tex]y=-3(1)+5\Rightarrow y=2[/tex]So, the value of y when x = 1 is 2.
*x = 2:
[tex]y=-3(2)+5\Rightarrow y=-1[/tex]So, the value of y when x = 2 is -1.
*x = 3:
[tex]y=-3(3)+5\Rightarrow y=-4[/tex]So, the value of y when x = 3 is -4.
***The table should look like this:
x | y
0 | 5
1 | 2
2 | -1
3 | -4
***The graph is:
what does this mean i dont get it please help me thanks, :)
Answers
It means that you are supposed to group The like terms together and simplify them
you will find that 2t is the liketerm with -5t and -u is a like term with -6u
As a results we have
[tex] = 2t - 5t - u - 6u \\ = - 3t - 7u[/tex]
as indicated I have shown you the answer .
good luck
A toy car that is 0.5 ft long is used to model the actions of an actual car that is 15 ft long. Which ratio shows the relationship between the sizes of the model and the actual car? A. 2:5 B. 5:2 C. 30:1 D. 1:30
Answers
A toy car that is 0.5 ft long is used to model the actions of an actual car that is 15 ft long. Which ratio shows the relationship between the sizes of the model and the actual car?
A. 2:5
B. 5:2
C. 30:1
D. 1:30
_____________________
0.5 ft the toy car: 15 the actual car
0.5*2 =1
15 *2 = 30
1: 30
_____________________________________
The ratio1:30 shows the relationship between the sizes of the model and the actual car
____________
Do you have any questions regarding the solution?
find the x value (6x+9)° (4x-19)°
Answers
In this problem m and n are parallel lines, and the first angle is an exteriar angle an the secon is a interior angle.
this two condition give us that the two angles are complementary anlges so the sum of them should be 180 so:
[tex]6x+9+4x-19=180[/tex]and we can solve for x so:
[tex]\begin{gathered} 10x-10=180 \\ 10x=180+10 \\ x=\frac{190}{10} \\ x=19 \end{gathered}[/tex]Two lines are shown on the grid below.Read the statements below about the graph of the two lines.Which statements are true about the two lines on the graph?A.I,II, and IV onlyB.II,III, and IV onlyC.II and III only D.I,II,III,and IV
Answers
Answer:
B. II, III, and IV only
Explanation:
Vertical lines have an undefined slope and the equation of these lines is x = c, where c is a constant value
Horizontal lines have a slope equal to 0 and the equation of these lines is y = c, where c is a constant value.
Therefore, the statements that are true about the graph are:
The equation of line b is y = -5
Line b has a slope of 0
The equation of line a is x = 3
Which phrase represents this expression?
5 + 4 ÷ 2
Responses
the product of 5 and the quotient of 4 and 2
the product of 5 and the quotient of 4 and 2
the product of 5 and 4 is divided by 2
the product of 5 and 4 is divided by 2
the sum of 5 and 4 is divided by 2
the sum of 5 and 4 is divided by 2
the sum of 5 and the quotient of 4 and 2
Answers
Reason
According to the PEMDAS rule, we multiply and divide before add and subtract
So we find the “quotient” or divide 4 by 2 first. Then we add 5 to the quotient which is a “sum” of 5 and quotient
A 33-inch piece of steel is cut into three pieces so that the second piece is twiceas long as the first piece, and the third piece is one inch more than five times thelength of the first piece. What is the length of the first piece?
Answers
Let;
x = the length of the first piece
y=the length of the second piece
z=the length of the third piece
From the question;
"the second piece is twice as long as the first piece" can be written in equation as:
y = 2x
"the third piece is one inch more than five times the length of the first piece"
can be written as :
z= 5x+ 1
Total length of the 3 pieces = 33
This implies:
x + y + z =33
substitute y=2x and z=5x+1 into the above
x + 2x + 5x+1 = 33
8x + 1 = 33
subtract 1 from both-side of the equation
8x = 33 -1
8x = 32
divide both-side of the equation by 8
x= 32/8
x= 4
The length of the first piece is 4-inches
Is the graph of the distance a person has driven over time an example of a continuous or discrete graph?
Answers
Let us first understand what are discrete and continuous variables.
Discrete variable:
A discrete variable is countable in a finite amount of time.
For example:
The number of coins in your pocket
The number of trees in the garden
It is not possible to have 2.5 coins or 7.3 trees
Continuous variable:
A continuous variable can take any numeric value.
For example:
The height of the tree
The room temperature
These values can be in decimal like 7.3, 0.23 etc
Now let us come to the question, the distance a person has driven can take any value
for example, it can be 50 miles or 23.4 miles or 120.5 miles
So, decimal values are possible
This means that it must be a continuous graph
The distance a person has driven over time an example of a continuous graph.
What is the mean and median of the data set
Answers
The mean of a data set is the sum of the data divided by the total number of data.
The median of a data set is the middle number in the set (after the numbers have been arranged from least to greatest, or, if there is an even number of data, the median is the average of the two middle numbers.
You have the next data set:
[tex]\begin{gathered} \lbrace11,11,11,11,12,12,12,13,13,13,13,13,13,14,15,15,15,15,15, \\ 15,16,16,16,16,16,17,17,17\rbrace \end{gathered}[/tex]A total of 28 data.
The mean is equal to the sum of the 28 numbers and then divided into 28:
[tex]undefined[/tex]b. Write
√x
as a single radical in simplest form.
5√x
Answers
Answer:
(tenth root of x to the third power)
see image
Step-by-step explanation:
To do this problem you need to know how to convert radicals to an expression with a fraction exponent(and back to radicals again), ALSO exponent rules for division ALSO subtracting fractions.
Square root x can be written as x^ 1/2
fifth root x can be written as x^ 1/5
When you are dividing expressions with the same base, exponent rules say to SUBTRACT the exponents.
1/2 - 1/5 change to common denominator
5/10 - 2/10
= 3/10
x^1/2 / x^1/5 =
x^ (1/2 - 1/5) =
x^ (5/10-2/10) =
x^ 3/10
Then change back to a radical. Remember "down and out" or "roots are down" and "up, up, up" or "exponents are up"
the number down below goes out (outside) the radical. And the number up top is up and exponents are up, up, up
see image.
x^3/10 =
tenth root (x^3)
see image.
Figure RSTU has coordinates R = (3,4), S = (7.2), T = (5, 10), and U = (12,8). The figure is dilated from the origin by a scale factor r . Select the correct coordinates of R. A R' = (3,2) B R' = (1.5, 4) C R' = (3.5, 4.5) D R' = (1.5, 2) * Select the correct answer. 1 point Ο Α OB D
Answers
Answer
Option D is correct.
R' (1.5, 2)
Explanation
A dilation means the size is increased or decreased. If the scale factor is less than 1, then the size is decreased, but if the scale factor is more than 1, it means the figure is enlarged.
Dilating about the origin just multiplies the coordinates by the scale factor. So, dilating (x, y) about the origin by a scale factor k, gives new coordinates (kx, ky).
For this question, we need to dilate R (3, 4) by a scale factor, r = ½
R' = [½(3), ½(4)] = (1.5, 2)
Hope this Helps!!!
Solve each equation for the variable. h/2 + 3.5 = 7.1
Answers
To answer this question, we can proceed as follows:
[tex]\frac{h}{2}+3.5=7.1[/tex]1. Subtract 3.5 to both sides of the equation:
[tex]\frac{h}{2}+3.5-3.5=7.1-3.5\Rightarrow\frac{h}{2}+0=3.6[/tex]2. Multiply by 2 to both sides of the equation:
[tex]2\cdot\frac{h}{2}=2\cdot3.6\Rightarrow h=7.2[/tex]We can check this result as follows:
[tex]\frac{7.2}{2}+3.5=3.6+3.5=7.1\Rightarrow7.1=7.1[/tex]This result is TRUE. Then, the value for h = 7.2.
Hi, can you help me to solve this problem please!
Answers
We have the following function
[tex]f(x)=7+6x[/tex]Now, we must replace the variable x by the given value, that is,
[tex]f(10)=7+6(10)[/tex]which gives
[tex]\begin{gathered} f(10)=7+60 \\ f(10)=67 \end{gathered}[/tex]Therefore, the answer is f(10)=67
how many pennies are in a dollar
Answers
Answer: 100
Step-by-step explanation:
$1 =100 pennies
he multiplication table below can be used to find equivalent ratios.
A multiplication table.
Which ratio is equivalent to the ratio 18:24?
15:20
20:15
30:36
36:30
Answers
Answer:
15:20
Step-by-step explanation:
18:24 can be written [tex]\frac{18}{24}[/tex] if I simplify this by dividing the top and bottom by 6, I get [tex]\frac{3}{4}[/tex]
I am looking for what other ration will reduce to [tex]\frac{3}{4}[/tex]
[tex]\frac{15}{20}[/tex] Divide the top and bottom by 5 and you will get [tex]\frac{3}{4}[/tex]
A 14 m long ladder is placed against a tree. The top of the ladder reaches a point
13 m up the tree.
How far away is the base of the ladder from the base of the tree?
Give your answer in metres (m) to 1 d.p.
Answers
Answer:
Approximately 5.2 meters
Step-by-step explanation:
This formation will make a right triangle. The ground to the point in the tree is one of the legs. The base of the tree to the base of ladder is another leg and the length of the ladder is the hypotenuse. In this case, we already have the hypotenuse and one of the legs, so we need to find the value of another leg.
We can do so by using the Pythagorean Theorem which is [tex]a^2+b^2=c^2\\[/tex].
a and b represent the values of the two legs, and c is the hypotenuse. Since we already have the hypotenuse, we can change this equation a bit to find the other leg.
Let's assign the missing value, b in the theorem.
The new equation will be [tex]b^2=c^2-a^2[/tex].
We can insert the values for c and a and solve for b.
The new equation will be [tex]b^2 = 14^2-13^2[/tex].
[tex]b^2=196-169[/tex]
[tex]b^2=27[/tex]
[tex]\sqrt{b^2} =\sqrt{27}[/tex]
The square root of [tex]b^2[/tex] cancels out.
The approximate square root of 27 is 5.19 which we can round to 5.2.