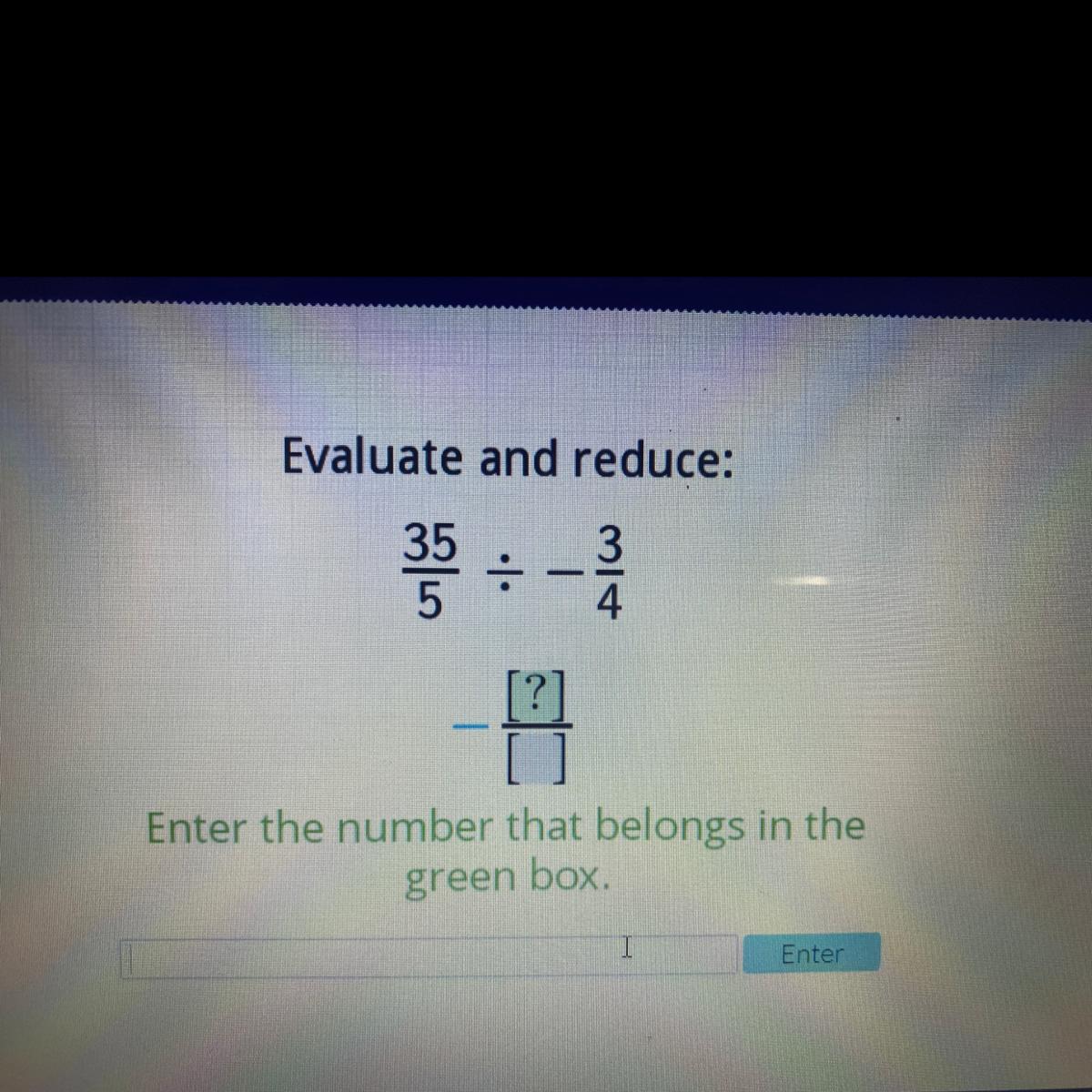
Evaluate and reduce:
3
4
35 - -
F
Enter the number that belongs in the
green box.

Answer:

The answer is

[tex] \huge y + 1 = 15(x - 3) \\ [/tex]

Step-by-step explanation:

To find an equation of a line in point slope form when given the slope and a point we use the formula

[tex]y - y_1 = m(x - x_1)[/tex]

where

m is the slope

( x1 , y1) is the point

From the question we have the final answer as

[tex]y + 1 = 15(x - 3)[/tex]

Hope this helps you

Answer:

(-3,3)

Step-by-step explanation:

Answer:

= -1/14

Step-by-step explanation:

We can use the slope formula

m = ( y2-y1)/(x2-x1)

    = ( -3 - -4)/( -6 -8)

   = ( -3+4)/( -6-8)

   1/-14

= -1/14

Answer:

(x-14)^2+(y-3)^2=9

Step-by-step explanation:

equation of a circle is (x-h)^2+(y-h)^2=r^2

so center is (14,3) and is tangent externally means

(x-14)^2+(y-3)2=3^2

(x-14)^2+(y-3)^2=9 answer

The equation of a circle is externally tangent to the given circle and has a center at (14, 3) is [tex](x-14)^2 + (y-3)^2=9[/tex]

The standard formula for finding the equation of a circle is expressed as:

[tex](x-a)^2+(y-b)^2=r^2[/tex]

where

(a, b) is the centre

r is the radius

Given the center at (14, 3)

If the equation of a circle is externally tangent to the given circle and has a center at (14, 3), then the radius will be 3

Substitute the radius and the centre into the expression above to have:

[tex](x-14)^2 + (y-3)^2=3^2\\(x-14)^2 + (y-3)^2=9[/tex]

Hence the equation of a circle is externally tangent to the given circle and has a center at (14, 3) is [tex](x-14)^2 + (y-3)^2=9[/tex]

Learn more here: https://brainly.com/question/24217736

Answer:

The probability that a person with restless leg syndrome has fibromyalgia is 0.183.

Step-by-step explanation:

Denote the events as follows:

F = a person with fibromyalgia

R = a person having restless leg syndrome

The information provided is as follows:

P (R | F) = 0.33

P (R | F') = 0.03

P (F) = 0.02

Consider the tree diagram attached below.

Compute the probability that a person with restless leg syndrome has fibromyalgia as follows:

[tex]P(F|R)=\frac{P(R|F)P(F)}{P(R|F)P(F)+P(R|F')P(F')}[/tex]

            [tex]=\frac{(0.33\times 0.02)}{(0.33\times 0.02)+(0.03\times 0.98)}\\\\=\frac{0.0066}{0.0066+0.0294}\\\\=0.183333\\\\\approx 0.183[/tex]

Thus, the probability that a person with restless leg syndrome has fibromyalgia is 0.183.

Answer:

the last 1

Step-by-step explanation:

Answer:

6 months is: 15675

2 months is: 5172.75

1 month is: 2586.37

15 months is: 38795.62

the missing number is: 12 months

Step-by-step explanation:

Answer:

66

Step-by-step explanation:

increase the number by 175% of its value.

percentage increase = 175% × 24

new value =

24 + percentage increase =

24 + (175% × 24) =

24 + 175% × 24 =

(1 + 175%) × 24 =

(100% + 175%) × 24 =

275% × 24 =

275 ÷ 100 × 24 =

275 × 24 ÷ 100 =

6,600 ÷ 100 =

66

Step-by-step explanation:

When metamorphic rock melts it turns into magma.

Answer:

about 172.82

Step-by-step explanation:

Answer:

83.23

Step-by-step explanation:

to work out surface area of a  right cone u

A=πr(r+h2+r2)

hope this helps

im not sure if its right tho

Answer:

163

Step-by-step explanation:

Answer:

the answer is 2x+y=4

Step-by-step explanation:

2x+y=4

Answer:

y = -2x + 4

Step-by-step explanation:

Answer:

8.64

Step-by-step explanation:

8.64

[tex]12\;percent\;of\;72=8.64[/tex]

Meaning lees 10 from 20 and multiply

Hi there!

First of all, let the unknown number be z.

Now, subtract 10:

z-10

This expression is equal to twice the same number:

z-10=2z

Solve this equation:

z-2z=10

-z=10

Divide both sides by -1 in order to get rid of the minus sign:

z=-10

Hope everything is clear.

Let me know if you have any questions!

#KeepLearning

:-)

Answer:

I think its B

Step-by-step explanation:

Forgive me if I am wrong, give me brainliest if I am right!

Answer:

-11

Step-by-step explanation:

This is the answer because:

1) First, multiply the negative sign with the positive sign.

Negative x Positive = Negative

Equation: -7 - 4

2) Now, multiply the negative sign with the negative sign.

Negative x Negative =  Positive  

Equation: 7 + 4 = 11

3) Finally, add the greater number's sign (-7) in front of the number.

-11

Hope this helps! :D

Answer:

The answer is "[tex]\bold{11000(0.83)^t}[/tex]".

Step-by-step explanation:

[tex]\bold{ \text{selling price}} = \$ 11,000 \\\\\bold{ \text{loses}} = 17 \%[/tex]

[tex]\bold{\to f(t)= c (1-r)^t} \\\\[/tex]

           [tex]=11,000 (1- 0.17)^t\\\\=11,000(0.83 )^t[/tex]

Answer:

5.625 inches

Step-by-step explanation:

Given that:

Total Rainfall in inches (P) = 8 inches

The runoff volume (in inches) Q = ???

The curve number CN = 80

Recall that: The runoff volume can be calculated by using the formula:

[tex]Q = \dfrac{(P-0.2S)^2}{(P+0.8S)}[/tex]    for P > 0.2S

Q = 0                     for P < 0.2S

[tex]S = \dfrac{1000}{CN}-10[/tex]

where:

curve number CN = 80

[tex]S = \dfrac{1000}{80}-10[/tex]

S = 2.5 inches

Since the rainfall (P) is greater than 0.25

Then:

[tex]Q = \dfrac{(P-0.2S)^2}{(P+0.8S)}[/tex]  

[tex]Q = \dfrac{(8-0.2(2.5))^2}{(8+0.8(2.5))}[/tex]

[tex]Q = \dfrac{(8-0.5)^2}{(8+2)}[/tex]

[tex]Q = \dfrac{(7.5)^2}{(10)}[/tex]

[tex]Q = \dfrac{(56.25)}{(10)}[/tex]

Q = 5.625 inches

Thus, the runoff volume = 5.625 inches

Answer:

Hello! I'm sorry I couldn't get to your question sooner. I just completed this quiz!

The equation of the circle that represents the dartboard is (x-10)^2 + (y-17/3)^2 = 9/16, where the origin is the lower-left corner of the room and the unit of the radius is feet.  

The position of Sasha's dart is represented by the coordinates (10.25,5). Sash's dart does land on the dartboard.

This quiz was completed on k12, lesson 3.03.

The question is an illustration of equation of circles.

From the question, we understand that:

[tex]\mathbf{h = 5\ ft\ 8\ in }[/tex] ---- the height at which the dartboard was hung

[tex]\mathbf{d = 18\i n }[/tex] ---- the diameter of the dartboard

[tex]\mathbf{B = 10ft}[/tex]  --- the bull's eye

[tex]\mathbf{D = (10.25ft, 5ft)}[/tex] --- Sasha's dart

Equation of the circle

First, we convert all units to feet

This is done by dividing inches units by 12

[tex]\mathbf{h = 5\ ft\ 8\ in }[/tex]

[tex]\mathbf{h = 5\ ft\ + \frac{8}{12}\ ft }[/tex]

[tex]\mathbf{h = 5\ ft\ + \frac{2}{3}\ ft }[/tex]

Take LCM

[tex]\mathbf{h = \frac{15 + 2}{3}\ ft }[/tex]

[tex]\mathbf{h = \frac{17}{3}\ ft }[/tex]

[tex]\mathbf{d = 18\i n }[/tex]

[tex]\mathbf{d = \frac{18}{12}ft}[/tex]

[tex]\mathbf{d = \frac{3}{2}ft}[/tex]

Divide by 2 to calculate radius

[tex]\mathbf{r = \frac{3}{2*2}ft}[/tex]

[tex]\mathbf{r = \frac{3}{4}ft}[/tex]

The equation of the circle is represented as:

[tex]\mathbf{(x - a)^2 + (y - b)^2 = r^2}[/tex]

In this case:

[tex]\mathbf{a = B = 10ft}[/tex] -- the distance between the bull's eye and the wall

[tex]\mathbf{b = h = \frac{17}{3}\ ft }[/tex] ---- the height at which the dartboard was hung

So, we have:

[tex]\mathbf{(x - a)^2 + (y - b)^2 = r^2}[/tex]

[tex]\mathbf{(x - 10)^2 + (y - \frac{17}3)^2 = (\frac 34)^2}[/tex]

Evaluate the exponents

[tex]\mathbf{(x - 10)^2 + (y - \frac{17}3)^2 = \frac 9{16}}[/tex]

Hence, the equation of the circle is: [tex]\mathbf{(x - 10)^2 + (y - \frac{17}3)^2 = \frac 9{16}}[/tex]

Does Sasha’s dart land on the dartboard?

Yes her dart lands on the dartboard because

[tex]\mathbf{D = (10.25ft, 5ft)}[/tex] is within the circumference of the dartboard

Read more about equation of circles at:

https://brainly.com/question/23988015

Answer:

t=8

Step-by-step explanation:

400 divided by 50 hopefully that helps with your question

Answer:

Number of $10 bills = 2

Number of $5 bills = 3

Number of $1 bills  = 5

Step-by-step explanation:

Given:

Total amount = $40

Number of $10 bills = x

Number of $5 bills = x + 1

Number of $1 bills = x + 1 + 2 = x + 3

Find:

Number of each bills

Computation:

10(x) + 5(x+1) + 1(x+3) = 40

10x + 5x + 5 + x + 3 = 40

16x = 32

x = 2

Number of $10 bills = x = 2

Number of $5 bills = x + 1 = 3

Number of $1 bills  = x + 3 = 5

Answer:

# of $10 bills = 2

# of $5 bills = 3

# of $1 bills  = 5

Step-by-step explanation:

Answer:

True

Step-by-step explanation:

There must be a constant of proportionality.

Hope this helps!

Answer:

12.2 12.3 12.4 12.5

Step-by-step explanation:

x^2 = 4 py

where p<0

Step-by-step explanation:

I think this is it but I am not sure

Answer:

The probability is   [tex]P(X  >300 ) = 0.97219 [/tex]

Step-by-step explanation:

From the question we are told that

 The capacity of  an Airliner  is  k =  300 passengers

 The sample size n =  320 passengers

  The probability the a randomly selected passenger shows up on to the airport

    [tex]p = 0.96[/tex]

Generally the mean is mathematically represented as

    [tex]\mu  =  n*  p[/tex]

  => [tex]\mu  =  320 *  0.96[/tex]

    => [tex]\mu  = 307.2[/tex]

Generally the standard deviation is  

    [tex]\sigma =  \sqrt{n *  p *  (1 -p ) }[/tex]

=>  [tex]\sigma =  \sqrt{320  *  0.96 *  (1 -0.96 ) }[/tex]

=> [tex]\sigma =3.50 [/tex]

Applying Normal approximation of binomial distribution

Generally the probability that there will not be enough seats to accommodate all passengers is mathematically represented as

  [tex]P(X  > k ) =  P( \frac{ X -\mu }{\sigma }  >  \frac{k - \mu}{\sigma } )[/tex]

Here [tex]\frac{ X -\mu }{\sigma }  =Z (The \ standardized \  value \  of  \ X )[/tex]

=>[tex]P(X  >300 ) =  P(Z >  \frac{300 - 307.2}{3.50} )[/tex]

Now applying  continuity correction we have

    [tex]P(X  >300 ) =  P(Z >  \frac{[300+0.5] - 307.2}{3.50} )[/tex]    

=>    [tex]P(X  >300 ) =  P(Z >  \frac{[300.5] - 307.2}{3.50} )[/tex]

=>    [tex]P(X  >300 ) =  P(Z >  -1.914 )[/tex]

From the z-table  

    [tex]P(Z >  -1.914 ) =  0.97219[/tex]

So

    [tex]P(X  >300 ) = 0.97219 [/tex]

Answer:

(f - g)(x) = -x - 6

(f + g)(x) = 3x - 4

(f*g)(4) = -9

Step-by-step explanation:

These are your equations:

f(x) = x - 5

g(x) = 2x + 1

To find (f - g)(x), subtract g(x) from f(x).

(f - g)(x) = x - 5 - (2x + 1)

(f - g)(x) = x - 5 - 2x - 1

(f - g)(x) = -x - 5 - 1

(f - g)(x) = -x - 6

To find (f + g)(x), add f(x) with g(x).

(f + g)(x) = x - 5 + 2x + 1

(f + g)(x) = 3x - 5 + 1

(f + g)(x) = 3x - 4

To find (f*g)(4), you need to first find (f*g)(4).  You can do this by multiplying f(x) wih g(x).

(f*g)(x) = (x - 5)(2x + 1)

(f*g)(x) = 2x² - 9x - 5

Now that you have (f*g)(x), solve with x as 4.

(f*g)(4) = 2(4)² - 9(4) - 5

(f*g)(4) = 2(16) - 9(4) - 5

(f*g)(4) = 32 - 36 - 5

(f*g)(4) = -9

The required expression for (f-g)(x), (f+g)(x) and (fg)(4) are given as 3x - 4, -x - 6 and 11.

Functions is the relationship between sets of values. e g y=f(x), for every value of x there is its exists in a set of y. x is the independent variable while Y is the dependent variable.

Here,
f(x)=x-5
g(x) = 2x+1

According to the question,
[f + g ](x) = x - 5 + 2x + 1 = 3x - 4

[f + g ](x) =  3x - 4

[f - g ](x) =  x - 5 - 2x - 1
[f - g ](x) = -x - 6

(f.g)(x) = (x - 5)(2x + 1)
(f.g)(x) = 2x² -4x -5

(f.g)(4) = 2[4]² - 4[4] - 5
         = 32 - 16 - 5
         = 11
(f.g)(4) = 11

Thus, the required expression for (f-g)(x), (f+g)(x) and (fg)(4) are given as 3x - 4, -x - 6 and 11.

Learn more about function here:

brainly.com/question/21145944

#SPJ2

Answer:

C

Step-by-step explanation:

1 back, 3 up.