Answers
To find:
The area of the shaded region.
Solution:
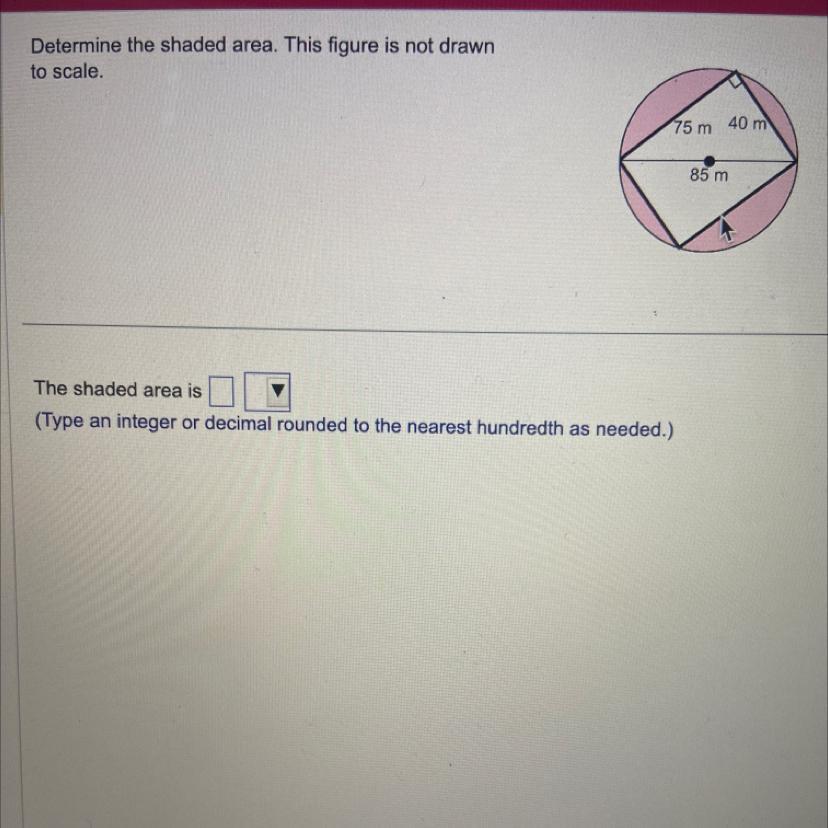
From the figure, it is clear that the length and width of the rectangle inside the circle are 75m and 40m. The diameter of the circle is 85m. The radius of the circle is 85/2m.
The shaded region is equals (area of the circle - area of the rectangle).
So, the area of the shaded region is:
[tex]\begin{gathered} A=\pi r^2-l\times w \\ A=\pi(\frac{85}{2})^2-75\times40 \\ A=\frac{22}{7}\times\frac{7225}{4}-3000 \\ A=\frac{158950}{28}-3000 \\ A=5676.79-3000 \\ A=2676.79m^2 \end{gathered}[/tex]Thus, the area of the shaded region is 2676.79 m^2.
Related Questions
The price of Stock A at 9 A.M. was $12.42. Since then, the price has been increasing at the rate of $0.12 each hour. At noon the price of Stock B was $12.92. It begins to decrease at the rate of $0.09 each hour. If the two rates continue, in how many hours will the prices of the two stocks be the same?
Answers
The hours when the prices of the two stocks be the same is 2.38 hours.
How to illustrate the information?From the information, the price of Stock A at 9 A.M. was $12.42 and the price has been increasing at the rate of $0.12 each hour. This will be the expressed as 12.42 + 0.12h.
At noon the price of Stock B was $12.92. It begins to decrease at the rate of $0.09 each hour. This will be:
= 12.92 - 0.09h
where h = number of hours
Equate both equations. This will be:
12.42 + 0.12h = 12.92 - 0.09h
Collect like terms
12.92 - 12.42 = 0.12h + 0.09h
0.21h = 0.50
h = 0.50 / 0.21
h = 2.38 hours.
Learn more about time on:
brainly.com/question/26046491
#SPJ1
Is Ari’s answer to the question, correct? If not, where did Ari make a mistake? If his answer is incorrect, explain what the correct answer is and why it is correct.
Answers
None of Ari's answer to the question is correct. The right application of the laws of exponents to get the correct answer is explained below.
What are the Laws of Exponents?Some of the laws of exponents can be summarized as follows.
The product law of exponents: This states that we are to add the exponents together if we are multiplying two numbers that have the same base. For example, [tex]x^m \times x^n = x^{m + n}[/tex].The division law of exponents: this states that when dividing two numbers that have the same base, we are to find the difference of their exponents. For example, [tex]\frac{x^m}{x^n} = x^{m - n}[/tex].The negative law of exponents: This state that, [tex]x^{-m} = \frac{1}{x^m}[/tex].Based on the above laws of exponents, none of Ari's answer is correct. Below are the correct way to solve the questions:
1. [tex]4^2 \times 4^5 = 4^{2 + 5} = 4^7[/tex]
2. [tex](2^{-5})^3 = 2^{-3 \times 5} = 2^{-15} = \frac{1}{2^{15}}[/tex]
3. [tex]\frac{(\frac{1}{4})^4 \times (\frac{1}{4})^5 }{(\frac{1}{4})^3} = \frac{(\frac{1}{4})^{4 + 5} }{(\frac{1}{4})^3} = \frac{(\frac{1}{4})^9 }{(\frac{1}{4})^3} = (\frac{1}{4})^{9 - 3}} = (\frac{1}{4})^6[/tex]
Learn more about laws of exponents on:
https://brainly.com/question/847241
#SPJ1
10)BONUSKelll walks into science class and they have 6 hershey kisses and 6 reese cups on a scale that reads82.4 ounces. She wants some chocolate so she eats 2 hersey kisses and 1 reese cup and now thescale reads 63.8 ounces.a) Define your variables and set up a system of equations.
Answers
Leah, this is the solution:
Variables:
Let x to represent the weight of one Hershey kiss
Let y to represent the weight of one Reese cup
System of equations:
6x + 6y = 82.4
4x + 5y = 63.8
______________
Let's multiply the second equation by - 3/2, therefore:
6x + 6y = 82.4
-6x - 15y/2 = -95.7
________________
-15/2 + 6 = -3/2
_________________
-3y/2 = -13.3
Dividing by -3/2 at both sides:
-3y/2 / -3/2 = -13.3 / -3/2
y = 8.87
______________
Replacing y in the first equation and solving for x:
6x + 6 * 8.87 = 82.4
6x + 53.22 = 82.4
Subtracting 53.22 at both sides:
6x +53.22 - 53.22= 82.4 - 53.22
6x = 29.18
Dividing by 6 at both sides:
6x/6 = 29.18/6
x = 4.86
_________________
In conclusion, one Hershey kiss weights 4.86 ounces and one Reese cup weights 8.87 ounces.
The following hyperbola has a horizontal transverse axis: (x + 2) (w+7)=11617
Answers
for the given hyperbola
[tex]\frac{(x+2)^2}{16}-\frac{(y+7)^2}{17}=1[/tex]We have the following graph. Visually we can see that this hyperbola does have a transverse axis, however you can do all the calculations to check it
[tex]\begin{gathered} \frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1 \\ h=-2 \\ k=-7 \\ a^2=16 \\ b^2=17 \\ c^2=16+17 \\ c=\sqrt[]{33}=5.7 \\ f_1=(h-c,k) \\ f_1=(-2-5.7,-7) \\ f_2=(-7.7,-7) \\ f_2=(3.7,-7) \\ y=-7\to\text{ is the ecuation of the transversal axis} \end{gathered}[/tex]As we can see y = -7 is a line parallel to the x axis, turning the transversal axis horizontal.
That is, this hyperbola does have a horizontal transverse axis and the answer is TRUE
The mayor of a town proposes to fence off a triangular area of a building that includes two sides of the building as shown below.Which distance, in feet could be the length of the proposed fence line?100280220130
Answers
Solution
Using triangle inequality
The triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the remaining side.
The fence line is the longest size
100, 130 can't be the answer
[tex]200+70=270[/tex]280 can't be the answer be ause the triangle inequality says it should be less than the sum
[tex]Z<\text{ X +Y}[/tex]Therefore, the correct answer is 220
need help please 16x=-44-4y
-8x=28+4y
Answers
Answer: (x,y)= (-2/5,-43/5)
Step-by-step explanation:
Surface area of a cone: S = πr² + πrl;solve for l.
Answers
Answer:
[tex]l=\frac{S-\pi r^{2}}{\pi r}[/tex]Explanation:
The surface area of a cone is calculated using the formula:
[tex]S=πr^2+πrl[/tex]We want to solve for l.
First, subtract πr² from both sides of the equation:
[tex]\begin{gathered} S-\pi r^2=\pi r^2-\pi r^2+\pi rl \\ S-\pi r^2=\pi rl \end{gathered}[/tex]Next, divide both sides by πr:
[tex]\begin{gathered} \frac{S-\pi r^2}{\pi r}=\frac{\pi rl}{\pi r} \\ l=\frac{S-\pi r^{2}}{\pi r} \end{gathered}[/tex]The equation solved for l is:
[tex]l=\frac{S-\pi r^{2}}{\pi r}[/tex]Solve the following system of equations graphically on the set of axes below. Plot two or more dotes on the graphy = 2x - 8 y = -x + 4
Answers
Given:-
[tex]y=2x-8,y=-x+4[/tex]To find the graphical representation.
So the graph of y=2x-8 is,
Also the graph of y=-x+4 is,
Combining we get the graph
So the point is (4,0).
17. A moving company charges a flat rate of $85 plus and additional $0.17 per mile driven. How far must the company drive to earn at least $100? Round to thenearest mile.x2 84x2 78x2 80x2 88
Answers
ANSWER
88
EXPLANATION
Let x be the miles driven and y be the earnings of the company when they drive for x miles.
If the company charges $0.17 per mile driven plus a flat rate of $85, then the total cost for moving x miles away is,
[tex]y=85+0.17x[/tex]Now, we have to find for how many miles, x, the company must drive to earn $100 or more,
[tex]85+0.17x\ge100[/tex]Subtract 85 from both sides,
[tex]\begin{gathered} 85-85+0.17x\geq100-85 \\ \\ 0.17x\ge15 \end{gathered}[/tex]And divide both sides by 0.17,
[tex]\begin{gathered} \frac{0.17x}{0.17}\ge\frac{15}{0.17} \\ \\ x\ge88.24 \end{gathered}[/tex]Hence, the company must drive for at least 88 miles to earn at least $100, rounded to the nearest mile.
Solve the following inequality: 6p - 15 < 33
Answers
WE are to solve an inequality, so we proceed to isolate the variable "p" on one side of the inequality symbol:
6 p - 15 < 33
we add 15 to both sides:
6 p < 33 + 15
6 p < 48
now divide both sides by 6 (notice that since 6 is a positive number, the division doesn't change the direction of the inequality)
p < 48/6
p < 8
So we need to highlight on the number line, the line that starts at "8" and goes all the way to the left (to minus infinity), and make sure that at the point "8" you draw an "empty" circle to indicate that the number 8 itself is NOT included in your set of solutions.
LaVelle is making a pitcher of caffe mocha. For each ounce of chocolate syrup, she uses 5 ounces of coffee. She wants to make 48 ounces of caffe mocha.
Let c represent the number of ounces of coffee, and let s represent the number of ounces of chocolate syrup used. Which of the following systems of equations models this situation?
Answers
The systems of equations which correctly models the situation as described is;
s = 5c ands + c = 48Which systems of equations correctly models the situation as described in the task content?It follows from the task content that the system of equations which models the production process of caffe mocha be determined.
As given in the task content;
Let c represent the number of ounces of coffee.Let s represent the number of ounces of chocolate syrup.Hence, since For each ounce of chocolate syrup, she uses 5 ounces of coffee, the situation can be represented algebraically as;
s = 5c.Also, since she wants to make 48 ounces of caffe mocha; we have;
s + c = 48.Therefore, the required system of equations is;
s = 5c ands + c = 48.Read more on system of equations;
https://brainly.com/question/13729904
#SPJ1
The following circle passes through the origin. Find the equation.
Answers
Answer
(x - 2)² + (y - 2)² = 8
Step-by-step explanation
The equation of the circle centered at (h, k) with radius r is:
[tex](x-h)^2+(y-k)^2=r^2[/tex]In this case, the center of the circle is the point (2, 2), then h = 2 and k = 2, that is,
[tex](x-2)^2+(y-2)^2=r^2[/tex]Given that the circle passes through the center, then the point (0, 0) satisfies the above equation. Substituting x = 0 and y = 0 into the equation and solving for r²:
[tex]\begin{gathered} (0-2)^2+(0-2)^2=r^2 \\ 4+4=r^2 \\ 8=r^2 \end{gathered}[/tex]Substituting r² = 8 into the equations, we get:
[tex](x-2)^2+(y-2)^2=8[/tex]Which point is part of the solution of the inequality y ≤ |x+2|-3A.(-1,-1)B.(1,0)C.(0,0)D.(0,1)
Answers
We are going to test all options to see which is true and false.
The one that is true will be the point that is part of the solution.
[tex]\begin{gathered} A) \\ (-1,-1) \\ y\leq\lvert x+2\rvert-3 \\ -1\leq\lvert-1+2\rvert-3 \\ -1\leq\lvert1\rvert-3 \\ -1\leq1-3 \\ -1\leq-2 \\ \text{Not true, so the point (-1,-1) is not a part of the solution} \end{gathered}[/tex]We will move to the next option and test:
[tex]\begin{gathered} B) \\ (1,0) \\ y\leq\lvert x+2\rvert-3 \\ 0\leq\lvert1+2\rvert-3 \\ 0\leq\lvert3\rvert-3 \\ 0\leq3-3 \\ 0\leq0 \\ \text{The above solution is true, so it is a point that is part of the solution.} \\ \text{The correct answer is option B.} \end{gathered}[/tex]13. slove for x so the [tex]f(x) = 5[/tex]
Answers
Solution
We have the following function given:
f(x) = -3x+5
And we need to do the following:
5= -3x+5
And if we subtract 5 in both sides we got:
0 =-3x
Dividing both sides by -3 we got:
[tex]\frac{0}{-3}=\frac{-3x}{-3}[/tex]And finally we got:
x= 0
Problem 17
17) f(-2)= 3
18) f(0)= 3
19) f(1)= 0
20) f(-1)= 5.2
match the function rule with the graph of the function (number 24)
Answers
It is given that the function is:
[tex]y=\frac{3}{4}\times4^x[/tex]Therefore y=0 then the value of x will be:
[tex]\begin{gathered} 0=4^x \\ x=-\infty \end{gathered}[/tex]Now at x=0, y will be:
[tex]y=\frac{3}{4}[/tex]at x=1, y will be:
[tex]y=\frac{3}{4}\times4=3[/tex]These 3 points that is (-inf,0),(0,3/4),(1,3) are on graph D.
Hence option D is coreect.
Twenty-five randomly selected students were asked the number of movies they watched the previous week. The results are as follows.
Answers
Given the table that shows the number of movies and the corresponding frequency, you can determine that the total frequency is:
[tex]Total\text{ }Frequency=25[/tex]By definition:
[tex]Relative\text{ }Frequency=\frac{Frequency}{Total\text{ }Frequency}[/tex]By definition, the Cumulative Frequency can be obtained by adding the corresponding frequency with the previous frequencies and dividing the sum by the Total Frequency.
Therefore, you can determine that:
- For:
[tex]Frequency=3[/tex]You know:
[tex]Relative\text{ }Frequency=\frac{3}{25}[/tex]And:
[tex]Cummulative\text{ }Relative\text{ }Frequency=\frac{3}{25}[/tex]- Given:
[tex]Frequency=8[/tex]You get:
[tex]Relative\text{ }Frequency=\frac{8}{25}[/tex]And:
[tex]Cummulative\text{ }Relative\text{ }Frequency=\frac{3+8}{25}=\frac{11}{25}[/tex]- Given:
[tex]Frequency=9[/tex]You get:
[tex]Relative\text{ }Frequency=\frac{9}{25}[/tex]And:
[tex]Cummulative\text{ }Relative\text{ }Frequency=\frac{3+8+9}{25}=\frac{4}{5}[/tex]- Given:
[tex]Frequency=4[/tex]You get:
[tex]Relative\text{ }Frequency=\frac{4}{25}[/tex]And:
[tex]Cummulative\text{ }Relative\text{ }Frequency=\frac{3+8+9+4}{25}=\frac{24}{25}[/tex]- Given:
[tex]Frequency=1[/tex]You get:
[tex]Relative\text{ }Frequency=\frac{1}{25}[/tex]And:
[tex]Cummulative\text{ }Relative\text{ }Frequency=\frac{3+8+9+4+1}{25}=\frac{25}{25}=1[/tex]Hence, the answer is:
Which statements describe one of the transformations performed on f(x) = x?to create g(x) - 3(x + 5)2 - 2? Choose all that apply.DA. A translation of 2 units to the leftI B. A vertical stretch with a scale factor of 3O C. A vertical stretch with a scale factor of3O D. A translation of 5 units to the left
Answers
Solution:
The Function transformation of f(x) is:
[tex]g(x)=f(x+c)+d[/tex]If c > 0, then the graph shift left f(x+c).
If c<0, then the graph shift right f(x-c)
If d > 0, then the graph shift up f(x) +d
If d < 0, then the graph shift down f(x) -d
When the given equation is:
[tex]f(x)=x^2[/tex]The transformation equation is given:
[tex]g(x)=3(x+5)^2-2[/tex]Then, the graph shifts down 2 units and shifts left 5 units.
Also, the vertical stretch with a scale factor 3.
Therefore, the correct options are B and D.
1. Abby baked 2-dozen brownies. She took 1 dozen to her scout meeting. Her family ate 8, and she put the rest in a container in the refrigerator. How can Abby find the number of brownies left in the refrigerator?
Answers
In order to determine the amount of brownies left in the refrigerator, subtract 8 from 12.
How many brownies are left in the refrigerator?If Abby bakes 2 -dozen brownies, she baked 24 brownies. There are 12 pieces in 1 dozen, thus if she bakes two dozens, she baked 24 brownies ( 12 x 2).
The amount of brownies left after she takes one dozen to school = amount baked - amount taken for the meeting
24 - 12 = 12
Amount left in the refrigerator : amount left after she took a dozen for the meeting - amount eaten by her family
12 - 8 = 4
To learn more about subtraction, please check: https://brainly.com/question/854115
#SPJ1
what is 2 to the 6 power
Answers
Find the distance d(P1, P2) between the given points P1 and P2: P1 =(0,0) P2 = (2,3)d(P1,P2) = (Simplify your answer using radical as needed)
Answers
Recall that given points (a,b) and (c,d) the distance between them would be
[tex]d=\sqrt[2]{(c\text{ -a\rparen}^2+(d\text{ -b\rparen}^2}[/tex]In our case we are given a=0,b=0,c=2,d=3. So the distance would be
[tex]d=\sqrt[2]{(2\text{ -0\rparen}^2+(3\text{ -0\rparen}^2}=\sqrt[2]{2^2+3^2}=\sqrt[2]{4+9}=\sqrt[2]{13}[/tex]so the distance between them is the square root of 13.
Please help me come you just tell me the answer I don’t really need you to explain
Answers
Given:
[tex]\begin{gathered} \angle JKL=65 \\ \angle KJL=50 \end{gathered}[/tex]Sum of the angle of any triangle is 180
So:
[tex]\begin{gathered} \angle JKL+\angle KJL+\angle KLJ=180 \\ 65+50+\angle KLJ=180 \\ \angle KLJ=180-(65+50) \\ \angle KLJ=180-115 \\ \angle KLJ=65 \end{gathered}[/tex]Then two sides are also equal.
[tex]\begin{gathered} 3x-2=x+10 \\ 3x-x=10+2 \\ 2x=12 \\ x=\frac{12}{2} \\ x=6 \end{gathered}[/tex]So the value of x is 6.
in the graph below line k,y=-x makes a 45 degree angle with the x and y axescomplete the following
Answers
step 1
The equation of line k is y=-x
The rule of the reflection across the line y=-x is equal to
(x,y) -------> (-y,-x)
so
we have the point (2,5)
Apply the rule
(2,5) -----> (-5,-2)
step 2
Reflection across the x axis
The rule of the reflection across the x axis is
(x,y) ------> (x,-y)
so
Apply the rule to the point (-5,-2)
(-5,-2) ------> (-5,2)
therefore
the answer is
(-5,2)Finding the mode and range of a data set Each day, Kaitlin records the number of news articles she reads. Here are her results for the last eight days. 7, 3, 8, 5, 7,7,7,8 Find the mode and the range for the data. Mode: Range: X 5 ?
Answers
Explanation:
The set of values are given below as
[tex]7,3,8,5,7,7,7,8[/tex]Mode:
This the data that occurs highest or the dat that has the highest frequency
Range:
The is the difference between the lowest val and the highest value
[tex]Range=highest-lowest[/tex]Hence,
The final answers are
[tex]\begin{gathered} mode=7(it\text{ occurs 4 times\rparen} \\ range=8-3=5 \end{gathered}[/tex]Hence,
The final answer is
[tex]\begin{gathered} mode=7 \\ Range=5 \end{gathered}[/tex]Marco states that 7.696696669...... is a rational numberbecause it is a repeating decimal. Is he correct? Justifyyour answer.Yes he is correct because it keeps going and going and it will go on forever and ever so that is my guess
Answers
The answer is NO, Marco is wrong.
The number 7.696696669.... has not a repeating decimal there is no a number that is repeating, like 0.6969696969... in the last number the 69 is repeating, in the Marco's number the decimal number change every time.
Hannah is saving money to buy some lirns. She invests $290 in a savings account that earns 7.6% interest, compounded annually. How much money will she have in her account after 2 years? Answer in dollars and round to the nearest cent.
Answers
Principal amount, P= $290.
Rate, r = 0.076
Time, t = 2
Therefore, the total amount in her account after 2 years is
[tex]A=P(1+\frac{r}{n})^{nt}[/tex]Hence,
[tex]\begin{gathered} A=290(1+0.076)^2 \\ =335.755 \end{gathered}[/tex]Therefore, the amount is 335.80 dollars.
That is, 335 dollars and 80 cents.
At the park there is a pool shaped like a circle. A ring-shaped path goes around the pool. Its inner radius is 7 yd and its outer radius is 9 yd.We are going to give a new layer of coating to the path. If one gallon of coating can cover 5v * d ^ 2 how many gallons of coating do we need? Note that coating comes only by the gallon, so the number of gallons must be a whole number. (Use the value 3.14 for pi.)
Answers
3. Define and find the value of the central angle theinscribed angle, and the arc associated with both.Central angle:namemeasureInscribed angle:namedoYmeasureArc:namemeasure
Answers
Given
Answer
Central angle
Name XOY
Measure 90
Inscribed angle
name XZY
Measure 45
Arc
name XY
Measure = circumference of circle/4
Select the graph for the solution of the open sentence. Click until the correct graph appears. Ix| + 3 > 3
Answers
Given the sentence;
[tex]\mleft|x\mright|+3>3[/tex]Subtracting 3 from both sides;
[tex]\begin{gathered} \mleft|x\mright|+3>3 \\ |x|+3-3>3-3 \\ \mleft|x\mright|>0 \end{gathered}[/tex]Given the absolute value of x to be greater than zero, the range of value of x is;
[tex]\begin{gathered} x>0 \\ or \\ x<0 \end{gathered}[/tex]Therefore, the correct graph of the solution is;
True or false the surface area of a sphere with a radius of 10 units is larger than the surface area of a cube with edge lengths of 10 units
Answers
The surface area of a sphere is given by
[tex]S_s=4\pi r^2[/tex]in our case r=10 units ( the radius). By substituting this value into the last formula, we have
[tex]S_s=4(3.1416)(10^2)[/tex]which gives
[tex]S_s=1256.64u^2[/tex]On the other hand, the surface area of a cube is given by
[tex]S_c=6L^2[/tex]where L is the length of one side, that is, L=10. Then, we have
[tex]\begin{gathered} S_c=6\cdot(10^2) \\ S_c=6\cdot100=600u^2 \\ S_c=600u^2 \end{gathered}[/tex]By comparing both results, we can see that the surface area of our sphere is larger than the surface area of the given cube. So the answer is TRUE.
Use the rectangle at the right to answer the following questions. a. Find the area of the entire rectangle. Show your work. b. Calculate the perimeter of the figure. Show your work.
Answers
Length of the entire rectangle = 12 + 5 = 17
Width of the entire rectangle = 6+4 = 10
Part a
Area of rectangle = Length x width
Area of the entire rectangle = 17 x 10 = 170 square units
Part b
Perimeter of rectangle = 2( length + width )
Perimeter of the entire rectangle = 2(17 + 10 )
=2 (27) = 54
Perimeter of the entire rectangle = 54 units
Length of the entire rectangle = 12 + 5 = 17
Width of the entire rectangle = 6+4 = 10
Part a
Area of rectangle = Length x width
Area of the entire rectangle = 17 x 10 = 170 square units
Part b
Perimeter of rectangle = 2( length + width )
Perimeter of the entire rectangle = 2(17 + 10 )
=2 (27) = 54
Perimeter of the entire rectangle = 54 units