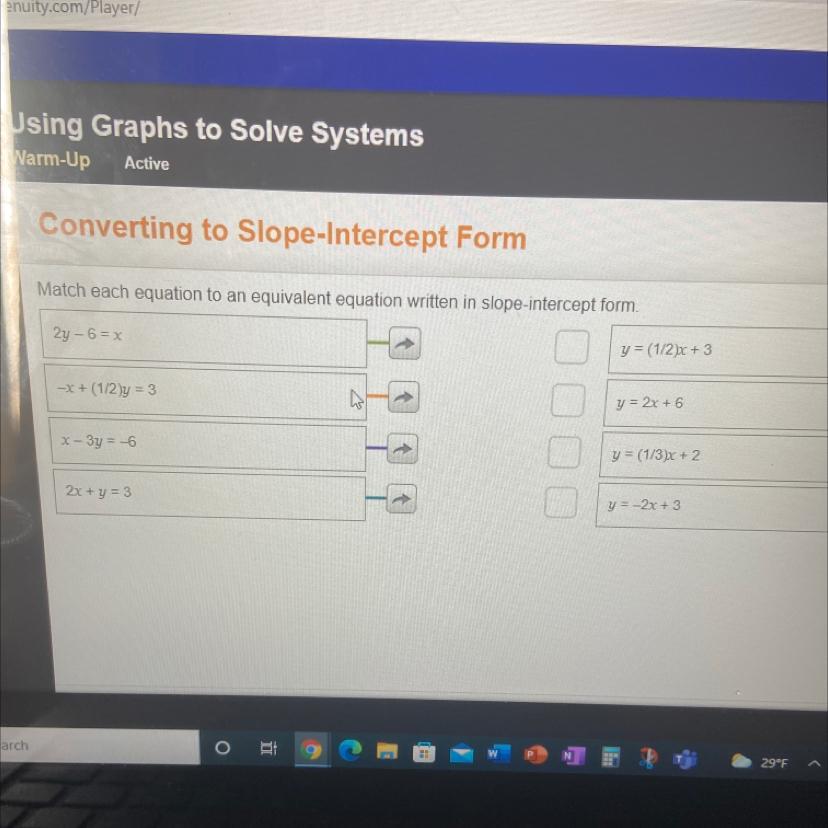
converting to slope intercept formmatch each equation to an equivalent equation written in slope intercept form.
Answers
Statement Problem: Match each equation to an equivalent equation written in slope-intercept form.
Solution:
A slope intercept form equation is written as;
[tex]y=mx+b[/tex](a)
[tex]2y-6=x[/tex]Add 6 to both sides of the equation;
[tex]\begin{gathered} 2y-6+6=x+6 \\ 2y=x+6 \end{gathered}[/tex]Divide each term by 2;
[tex]\begin{gathered} \frac{2y}{2}=\frac{x}{2}+\frac{6}{2} \\ y=(\frac{1}{2})x+3 \end{gathered}[/tex](b)
[tex]undefined[/tex]Related Questions
what is the answer to 65y=12
Answers
In this case, we have a equation with one unknown value (y)
all you have to do is to isolate y
Let's see
65 y=12
[tex]\begin{gathered} 65y=12 \\ \text{divide each side by }65 \\ \\ \frac{65y}{65}=\frac{12}{65} \\ \\ y=\frac{12}{65} \\ \end{gathered}[/tex]so the solution is y=12/65
I really hope it helps
Can someone help me out??
Answers
The correct option for the missing sides of given triangles is-
Part 1: x = 30Part 2: x = 21Part 3: x = 49Part 4: x = 22What is termed as the similar triangles?If two triangles' corresponding angles seem to be congruent and their corresponding sides are proportional, they are said to be similar. In other phrases, similar triangles have the same shape but may or may not be the same size.For the given question,
The dimension of the two triangles are given with the missing sides.
Part 1: In the given rectangles;
5/3 = x/18
x = 30
Part 2: In the given rectangles;
9/x = 3/7
x = 21
Part 3: In the given triangles;
x/63 = 7/9
x = 49
Part 4: In the given triangles;
16/x = 8/11
x = 22
Thus, the missing sides of the given shapes are found.
To know more about similar triangles, here
https://brainly.com/question/14285697
#SPJ13
A team won 5 and lost 2 of their first 7 games. The team continued to win at this rate and won w games in the 28-game season. Which of the following proportions could be used to determine w? 2. 7 28 B 2 5 28 5 7 28 D U NICT 28
Answers
Answer:
C. 5/7 = w/28
Explanation:
We're told from the question, the team won 5 and lost 2 of their first 7 games and later continued to win at this rate and won w games in the 28-game season.
Since w represents the number of games won in a 28-game season, in order to create a proportion to determine the value of w, we have to consider the number of games won (which was 5) in 1st 7 games.
So the proportion can then be written as;
[tex]\frac{5}{7}=\frac{w}{28}[/tex]What is the unit digit of 8433165483 x 946621539 x 5514381138
Answers
The value of the unit digit 8433165483 x 946621539 x 5514381138 will be6.
What is the fundamental principle of multiplication?Multiplication is the mathematical operation that is used to determine the product of two or more numbers. If an event can occur in m different ways and if following it, a second event can occur in n different ways, then the two events in succession can occur in m × n different ways.
For getting a number, we will first multiply each digit by its position and then;
8433165483 x 946621539 x 5514381138
Which is;
3 x 9 x 8
= 27 x 8 = 216
Therefore, the unit digit number will be 6.
Learn more about multiplications;
https://brainly.com/question/14059007
#SPJ1
If tan=21/20,0
a. sin a/2
b. cos a/2
c. tan a/2
Answers
Using trigonometry we can conclude that the value is sin a/2=7/58, cos a/2= -3/√58, tan a/2= -7/3.
What is Trigonometry?A branch of mathematics called trigonometry looks at how triangle side lengths and angles relate to one another. Applications of geometry to astronomical research led to the development of the field in Hellenistic civilization during the third century BC.We are aware:
x=tan(a/2)And,
tan(a)=2tan(a/2)/1-tan²(a/2)=21/20= 2x/1x2⇒21−21x²=40x⇒21x²+40x−21=0⇒21x²+49x−9x−21=0⇒7x(3x+7)−3(3x+7)=0⇒(3x+7)(7x−3)=0Thus, x=7/3 or x=3/7
It is now given:
180<a<270⇒ 90<a/2<135The a/2 second quadrant.
As a result:
x = tan(a/2)negativeTherefore,
x = tan(a/2)= -7/3sin(a/2) => +veThis means that:
sin(a/2) = 1/cos(a/2) = 1/(1+cot²(a/2))= 1/(1+1/tan(a/2))=1/√(1+9/49)=7/√58The formula is now:
cos(a/2)=sin(a/2)/tan(a/2)=7/√58/ -7/3cos(a/2) = -3/√58Therefore, using trigonometry we can conclude that the value is sin a/2=7/58, cos a/2= -3/√58, tan a/2= -7/3.
To learn more about Trigonometry click on the link
brainly.com/question/24349828
#SPJ13
I’ve been working on these similar questions but coming to this question. I found myself being stuck.
Answers
Solution:
If the variation in pressure is P pounds per square inch, then the Loudness L in decibels is;
[tex]L=20\log _{10}(121.3P)[/tex]When L=115 decibels;
[tex]\begin{gathered} 115=20\log _{10}(121.3P) \\ \text{Divide both sides by 20;} \\ \frac{115}{20}=\frac{20\log_{10}(121.3P)}{20} \\ \log _{10}(121.3P)=5.75 \end{gathered}[/tex]But from the logarithmic law, we have;
[tex]\log _ba=c\leftrightarrow a=b^c[/tex]Thus,
[tex]\begin{gathered} \log _{10}(121.3P)=5.75 \\ 121.3P=10^{5.75} \\ 121.3P=562341.33 \end{gathered}[/tex][tex]\begin{gathered} \text{Divide both sides by 121.3;} \\ \frac{121.3P}{121.3}=\frac{562341.33}{121.3} \\ P\cong4635.95 \end{gathered}[/tex]FINAL ANSWER:
[tex]4636.0\text{ pounds per square inch.}[/tex]Solve for the hypotenuse and then determine the ratios below (show all work)
Answers
hypotenuse=29
[tex]\sin x=\frac{20}{29}[/tex][tex]\cos y=\frac{20}{29}[/tex]
Explanation
Step 1
a) hypotenuse
to find the hypotenuse we can use the Pythagorean theorem ,it statse that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)
so
[tex]\begin{gathered} 21^2+20^2\text{= hypotenuse}^2 \\ 441+400=\text{ hypotenuse}^2 \\ 841=\text{hypotenuse}^2 \\ taking\text{ the square root in both sides} \\ \sqrt{841}=\sqrt{(hypotenuse)^2} \\ 29=hypotenuse \end{gathered}[/tex]so
hypotenuse=29
Step 2
now, sin x
the sin of an angle is the ratio of the opposite side ( the one in front of the angel) to the hypotenuse
[tex]\sin\theta=\frac{opposite\text{ side}}{hypotenuse}[/tex]hence, replace
[tex]\sin x=\frac{20}{29}[/tex]Step 3
finally, cos of y
the cos of an angle is the ratio of the adjancent side( the side the makes the angle) to the hypotenuse
[tex]cos\theta=\frac{adjacent\text{ side}}{hypotenuse}[/tex]so,replace
[tex]\cos y=\frac{20}{29}[/tex]I hope this helps you
In the equation Q = 45e1.031a quantity Q is changing over time t.(a) What is the quantity at timet = 0?(b) Is the quantity increasing or decreasing over time?(c) What is the percent per unit time continuous growth or decay rate?
Answers
(a) The equation is given as Q=45e^1.03t
where e=2.718
Taking t=0 the equation will be :
[tex]Q=45e^{1.03\ast0}[/tex]This will give;
[tex]Q=45\ast2.718^0[/tex]Q=45
find the sum of all two-digit natural numbers which are not divisible by 3。Want formulas and algorithms
Answers
The sum of all two-digit numbers which are not divisible by 3 is 2240.
What is Arithmetic progression?
An arithmetic sequence or progression is defined as a sequence of numbers in which for every pair of consecutive terms, the second number is obtained by adding a fixed number to the first one.
The sum of two-digit number in AP is Sn = n/2[2a+(n-1)d]
First, sum of two digit number 10, 11.....99 is
n = 90, a = 10 an= 99
Sn = n/2[2a+(n-1)d]
Sn = 90/2[2(10)+(90-1)1]
Sn = 45[20+89]
Sn= 4905
Now, the sum of two digit number divisible by 3 =
12, 15,...99
a = 12, n = 30, d = 3
Sn = n/2[2a+(n-1)d]
Sn=30/2[2(12)+(30-1)3]
Sn= 1665
Hence, sum of two digit number not divisible by 3 are 4905-1665
=2240
To know more about arithmetic progression, visit:
https://brainly.com/question/16904280
#SPJ9
Find The measure of the indicated to the nearest angle
Answers
The given figure is a right triangle, then we can apply the sine function to find the missing angle, so:
[tex]\sin\theta=\frac{opposite}{hypotenuse}[/tex]The opposite side to the angle measures 17, and the hypotenuse measures 19.
By replacing these values, we can find the angle:
[tex]\begin{gathered} \sin\theta=\frac{17}{19} \\ \\ \theta=\sin^{-1}(\frac{17}{19}) \\ \\ \theta=63.47 \\ \theta\approx64\degree \end{gathered}[/tex]The answer is 64°.
What is the value of x in the equation7 (4x + 1) – 32 5.7 · 13?X=
Answers
Given
[tex]\begin{gathered} 7(4x+1)-3x=5x-13 \\ 28x+7-3x=5x-13 \\ 25x-5x=-13-7 \\ 20x=-20 \\ x=-1 \end{gathered}[/tex]cost to rent a paddle boat at the city park includes a intentral fee of $7.00, plus $3.50 per hour. Which equation models the relationship between the total cost, y, and the number of hours, X, that the paddle boat is rentedA. y = 3.5x + 7. B. y = 7x + 3.5C. y = x/7 + 3.5. D. y = x/3.5 + 7
Answers
The total cost is represented as y, and the number of hours as x.
The intentral fee is $7.00.
Since the cost is $3.50 per hour, the total cost is
y=3.5x+7.
Hence, option A is correct.
which of the following are like terms3y^5, 2x^53y^5, 2y^56y^2, 2 z3y^4, 4x^3
Answers
In this case the answer is very simple.
3y^5, 2y^5 are like terms.
Because the variables and their exponents are the same.
(2-5). (6.0)Find the midpoint
Answers
Let:
(x1,y1)=(2,-5)
(x2,y2)=(6,0)
The midpoint is given by:
[tex]\begin{gathered} xm=\frac{x1+x2}{2} \\ xm=\frac{2+6}{2} \\ xm=\frac{8}{2}=4 \\ ym=\frac{-5+0}{2}=-\frac{5}{2}=-2.5 \end{gathered}[/tex]Therefore the midpoint is:
M = (4 , -5/2) or M = (4, -2.5)
Quinton will flip a coin and roll a die.What is the probability that he will flip "tails" and roll a "2
Answers
Answer:
there is a 50 percent chance he will land tails, and about a 33 percent chance he will rol a 2
Step-by-step explanation:
The table shows claims and their
probabilities for an insurance
company.
Amount of claim
(to the nearest $20,000)
$0
$20,000
$40,000
$60,000
$80,000
$100,000
Probability
0.70
0.16
0.09
0.03
0.01
0.01
Answers
Answer:
Step-by-step explanation:
This is an equation! Solutions: x=1.
Graphical form: Equation 3%2Ax-x%2B2=4 was fully solved.
Text form: 3*x-x+2=4 simplifies to 0=0
Cartoon (animation) form: simplify_cartoon%28+3%2Ax-x%2B2=4+%29
For tutors: simplify_cartoon( 3*x-x+2=4 )
If you have a website, here's a link to this solution.
For the situation select expression or equation that is not equivalent to the rest.A $79 hoodie is on sale for 25% off.
Answers
Given:
$79 hoodie is on sale for 25% off
We can solve or express this in many ways;
If it is 25% off, then the price is;
(100% - 25%) x 79
= (75%) x 79
= (0.75) (79)
OR
The price is;
79 - 25%(79)
= 79 - (0.25)(79)
OR
0.75 x 79 is the same as;
(1 - 0.25)(79)
Therefore, the expression or equation that is NOT equivalent to the rest is
25/100 (79)
Write this trinomial in factored form. 5a² - 30 - 14
Answers
replace x with a for this exercise
we use this formula to factor
[tex]x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}[/tex]where a=5, b=-3 and c=-14
[tex]x=\frac{-(-3)\pm\sqrt[]{(-3)^2-4(5)(-14)}}{2(5)}[/tex][tex]\begin{gathered} x=\frac{3\pm\sqrt[]{9+280}}{10} \\ \\ x=\frac{3\pm\sqrt[]{289}}{10} \\ \\ x=\frac{3\pm17}{10} \end{gathered}[/tex]we have two roots
[tex]\begin{gathered} x=\frac{3+17}{10} \\ x=2 \end{gathered}[/tex]and
[tex]\begin{gathered} x=\frac{3-17}{10} \\ \\ x=-\frac{7}{5} \end{gathered}[/tex]so the simplified equation is
[tex](x-2)(x+\frac{7}{5})[/tex]now replace x for a
[tex](a-2)(a+\frac{7}{5})[/tex]the sugar sweet company is going to transport its sugar to market. it will cost 7500 to rent trucks,and it will cost an additional 225 for each ton of sugar transportlet C represent the total cost (in dollars) and let s represent the amount of sugar ( in tons ) transported. write an equation relating C to S. then use this equation to find the total cost to transport 18 tons of suger.
Answers
Given that a sugar sweet company costs to transport its sugar, 7500 to rent truck and additional 225 for each ton.
[tex]undefined[/tex]
By what factor does the population grow every 2 years? Use rhis information to fill out the table.By what factor does the population grow every year? explain how you know, and use this information to complete the table.
Answers
From the table, we see that:
• Year 0 has a population of 10,
,• Year 2 has a population of 20.
So after two years, the population of fish is doubled.
1) By year 4, we will have double the population of year 2, so the population will be 2*20 = 40.
2) To function that describes the growth of the population is:
[tex]P(t)=P_0\cdot r^t._{}[/tex]Where P_0 is the initial population and r is the growth factor.
We know that after two years, the population of fish is doubled:
[tex]P(t+2)=2\cdot P(t)\text{.}[/tex]Using the formula above evaluated in t + 2, we have:
[tex]P(t+2)=P_0\cdot r^{t+2}=(P_0\cdot r^t)\cdot r^2=P(t)\cdot r^2[/tex]Equalling the last two equations, we have:
[tex]P(t+2)=2\cdot P(t)=P(t)\cdot r^2\text{.}[/tex]Solving for r the last equation, we have:
[tex]\begin{gathered} 2=r^2, \\ r=\sqrt[]{2}\text{.} \end{gathered}[/tex]So the growth factor is r = √2.
Answer:
1. 40
2. √2
110,169 is larger than 110,72
Answers
110,169 is larger than 110,72
This is false as the first decimal of 110.169 is 1 and the first decimal of 100,72 is 7.
110,169 is larger than 110,72
This is false as the first decimal of 110.169 is 1 and the first decimal of 100,72 is 7.
Find the slope of the line that passes through (8, 7) and (6, 2).
Answers
[tex]m = \frac{y2 - y1}{x2 - x1} \\ m = \frac{2 - 7}{6 - 8} \\ m = \frac{ - 5}{ - 2} \\ m = \frac{5}{2} [/tex]
ATTACHED IS THE SOLUTION WITH THE FORMULA TO CALCULATE THE SLOPE BETWEEN POINTS.
Find the slope of the tangent line when x=3 using the limit definition f(x) = X^2 - 5
Answers
SOLUTION
From the limit definition, we have that
[tex]f^{\prime}(x)=\lim _{h\to0}\frac{f(x+h)-f(x)}{h}[/tex]Now applying we have
[tex]\begin{gathered} f\mleft(x\mright)=x^2-5 \\ f^{\prime}(x)=\lim _{h\to0}\frac{f(x+h)-f(x)}{h} \\ =\lim _{h\to0}\frac{((x+h)^2-5)-(x^2-5)}{h} \\ =\lim _{h\to0}\frac{x^2+2xh+h^2^{}-5-(x^2-5)}{h} \\ =\lim _{h\to0}\frac{x^2+2xh+h^2-5-x^2+5}{h} \\ =\lim _{h\to0}\frac{x^2-x^2+2xh+h^2-5+5}{h} \\ =\lim _{h\to0}\frac{2xh+h^2}{h} \end{gathered}[/tex]factorizing for h, we have
[tex]\begin{gathered} =\lim _{h\to0}\frac{h(2x+h)^{}}{h} \\ \text{cancelling h} \\ =\lim _{h\to0}2x+h \\ =2x \end{gathered}[/tex]So, when x = 3, we have
[tex]\begin{gathered} =2x \\ =2\times3 \\ =6 \end{gathered}[/tex]Hence, the answer is 6
what is 3 8/9 + 8 1/2
Answers
Reflect triangle YWZ across line YW. Which of these is a valid reason why the image of Z will coincide with X?
Answers
Triangle WYZ
line YW
then YW is a bisector of, ZX
Find the value of z that makes quadrilateral EFGH a parallelogram.2zz+10FEHGz=Submit
Answers
In a parallelogram opposite sides have the same length therefore, for figure EFGH to be a parallelogram we must have that:
[tex]GF=HE[/tex]Substituting we get:
[tex]z+10=2z[/tex]Now, we solve for "z". First, we subtract "z" from both sides:
[tex]\begin{gathered} z-z+10=2z-z \\ 10=z \end{gathered}[/tex]Therefore, the value of "z" is 10.
Kia rides her bicycle at 20 miles per hour. Which equation represents the situation? Leth represent the hours traveled. Let d represent the distance traveled. Od 2012 Oh= 200 Od 20 h O h = 20 -
Answers
Velocity= 20 miles/hour
What is the procedure for 31/4-17/8= I'm getting 25/8
Answers
Evaluate the value of the expression:
[tex]3\frac{1}{4}-1\frac{7}{8}[/tex]Step 1: The mixed fraction will be converted to improper fraction
[tex]\begin{gathered} 3\frac{1}{4}-1\frac{7}{8} \\ =\frac{3\times4+1}{4}-\frac{1\times8+7}{8} \\ =\frac{12+1}{4}-\frac{8+7}{8} \\ =\frac{13}{4}-\frac{15}{8} \end{gathered}[/tex]Step 2: The denominator of 8 will be used as the L.C.M, since it's the greatest of the two
[tex]\begin{gathered} \frac{13}{4}-\frac{15}{8} \\ =\frac{26-15}{8} \\ =\frac{11}{8} \\ =1\frac{3}{8} \end{gathered}[/tex]Hence the correct answer = 1 3/8
[tex]1\frac{3}{8}[/tex]I need help the right side box are the answer choices
Answers
Statement: JKLM is a parallelogram
Reason - Give
Statement:
[tex]JK\parallel LM,\text{ }KL\parallel MJ[/tex]Reasons:
Definition of a parallelogram.
Statement:
[tex]\angle1\cong\angle2,\angle3\cong\angle4[/tex]Reasons:
Alternate interior angle theorem.
Statement:
[tex]Jl\cong Jl[/tex]Reasons:
Reflexive Propert
Statement:
[tex]\Delta JKL\cong\Delta LMJ[/tex]Reasons:
ASA
Statement:
[tex]JK=LM,KL=MJ[/tex]Reasons:
CPCTC
f (x+2) - 3o vertical shiftvertical stretchhorizontal reflectionhorizontal shiftvertical compressionhorizontal stretchhorizontal compressionvertical reflection
Answers
ANSWER:
[tex]\begin{gathered} (5x+3)\cdot(x+4) \\ x=-\frac{3}{5}\text{ and }x=-4 \end{gathered}[/tex]STEP-BY-STEP EXPLANATION:
We have the following function:
[tex]5x^2+23x+12[/tex]we factor and calculate the roots like this:
[tex]\begin{gathered} (5x+3)\cdot(x+4) \\ (5x+3)=0\rightarrow x=-\frac{3}{5} \\ (x+4)=0\rightarrow x=-4 \end{gathered}[/tex]Therefore the factored form would be
[tex](5x+3)\cdot(x+4)[/tex]And the roots of the functions are - 3/5 and -4