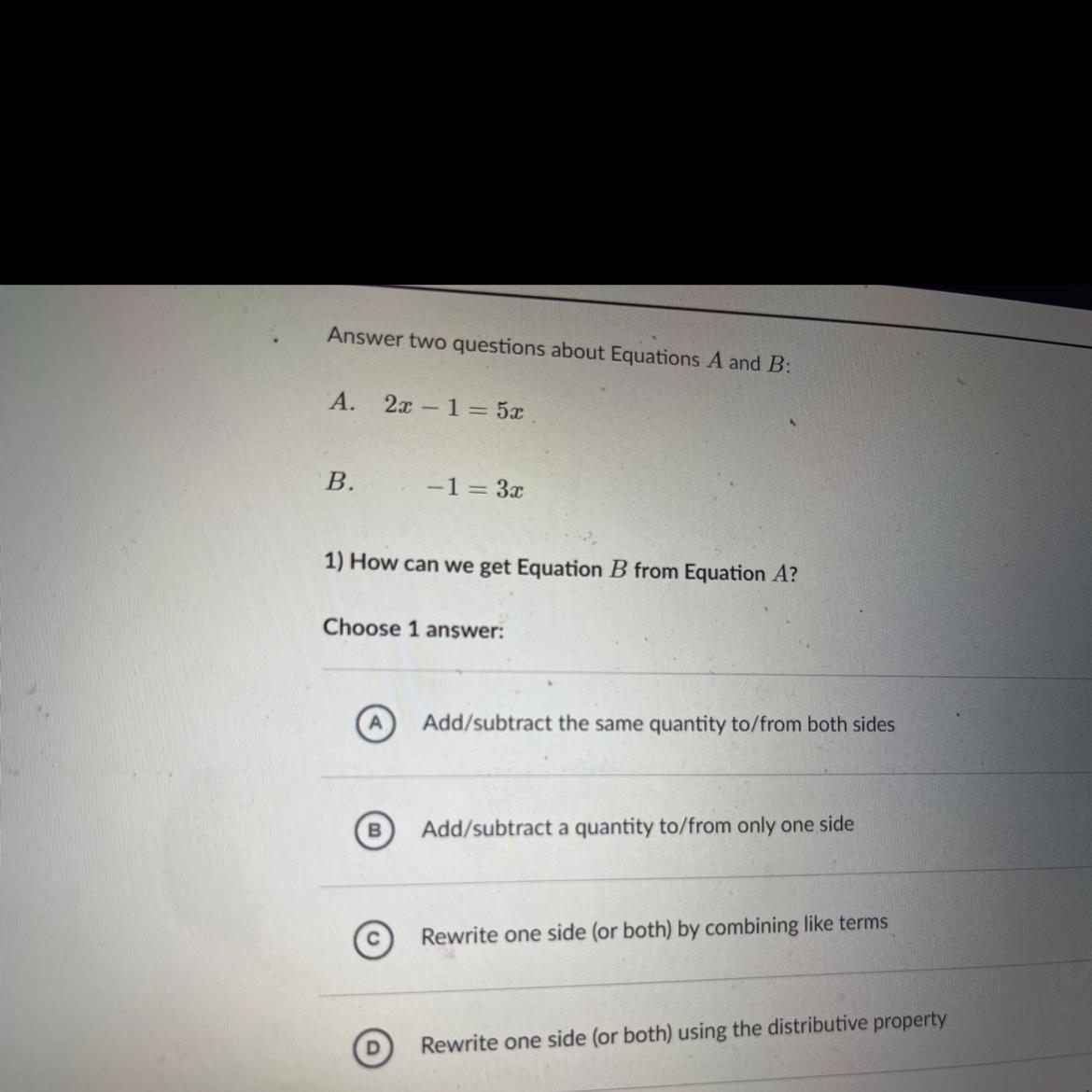
Answer two questions about Equations A and B
A. 2r-1= 5x
B. -1 = 3x
1) How can we get Equation B from Equation A?
Choose 1 answer:
Add/subtract the same quantity to/from both sides
Add/subtract a quantity to/from only one side
Rewrite one side (or both) by combining like terms
Rewrite one side (or both) using the distributive property
Answers
In the given equation A, we can (A) subtract the same quantity from both sides.
What are equations?In a mathematical equation, the equals sign is used to express that two expressions are equal. An equation is a mathematical statement that contains the symbol "equal to" between two expressions with identical values. Like 3x + 5 = 15, for example. There are many different types of equations, including linear, quadratic, cubic, and others. The three primary forms of linear equations are point-slope, standard, and slope-intercept.So, obtain equation B from equation A:
Equation A: 2x - 1 = 5xEquation B: -1 = 3xWe can subtract (2x) from both sides to get equation B as follows:
2x - 1 = 5x2x - 2x - 1 = 5x - 2x-1 = 3xTherefore, in the given equation A, we can (A) subtract the same quantity from both sides.
Know more about equations here:
https://brainly.com/question/28937794
#SPJ13
Related Questions
The Muffin Shop makes no-fat blueberry muffins that cost $.70 each. The Muffin Shop knows that 15% of the muffins will spoil. If The Muffin Shop wants 40% markup on cost and produces 800 muffins, what should The Muffin Shop price each muffin?
Answers
If The Muffin Shop wants a 40% markup on cost and produces 800 muffins, The Muffin Shop should price each muffin at $1.15.
How is the price determined?The total expected revenue is divided by the total unspoiled units sold to determine the selling price.
This is illustrated below.
Cost per unit of muffins = $0.70
The spoilage rate = 15%
Expected markup on cost = 40%
The total production units = 800 muffins
The total good units sold = 680 (800 x 1 - 15%)
Total cost for 800 units = $560 (0.70 x 800)
The markup on cost = $224 ($560 x 40%)
The total expected sales revenue = $784 ($560 + $224)
Seling price per unit = $1.15 ($784/680)
Thus, The Muffin Shop should price each muffin at $1.15 to meet its goals.
Learn more about pricing with the markup at https://brainly.com/question/1153322
#SPJ1
Please help, algebra 1, i dont know how to begin to solve it :/ thank you thank you.Simplify:
Answers
Given the expression:
[tex](x^2-4x^3)+(5x^3+3x^2)[/tex]You can simplify it as follows:
1. Distribute the positive sign. Since the sign between the parentheses is positive, it does not change the signs of the second parentheses:
[tex]=x^2-4x^3+5x^3+3x^2[/tex]2. Add the like terms.
By definition, like terms have the same variables with the same exponent.
In this case, you need to add the terms with exponent 3 and add the terms with exponent 2. Notice that:
[tex]\begin{gathered} -4x^3+5x^3=x^3 \\ \\ x^2+3x^2=4x^2 \end{gathered}[/tex]Then, you get:
[tex]=x^3+4x^2[/tex]Hence, the answer is:
[tex]=x^3+4x^2[/tex]m(x)=-x^2+4x+21. prove the zeros and determine the extreme value algebraically
Answers
The zeros of the function are:
[tex]\begin{gathered} -(x+3)(x-7)=0 \\ x=-3 \\ or \\ x=7 \end{gathered}[/tex]The vertex is a point V(h,k) on the function. It's either at the base or the top of the function, depending upon wether it opens, upward or downward respectively.
For a function of the form:
[tex]\begin{gathered} y=ax^2+bx+c \\ \text{The vertex(extreme value) is:} \\ h=\frac{-b}{2a} \\ k=y(h) \end{gathered}[/tex]Therefore:
[tex]\begin{gathered} m(x)=-x^2+4x+21 \\ a=-1 \\ b=4 \\ c=21 \\ h=\frac{-4}{2(-1)}=\frac{-4}{-2}=2 \\ k=m(h)=-(2)^2+4(2)+21=-4+8+21=25 \end{gathered}[/tex]Hence, the extreme value is 25 at x = 2
That's it, do you have any question?
The graph used Is below ill attach a picture of the question and options after
Answers
Using the triangle sum theorem:
[tex]\begin{gathered} m\angle L+m\angle K+20=180 \\ 2m\angle L=180-20 \\ 2m\angle L=160 \\ m\angle L=\frac{160}{2} \\ m\angle L=80 \end{gathered}[/tex]Using the exterior angle theorem:
[tex]\begin{gathered} m\angle E=m\angle L+m\angle J \\ m\angle E=80+20 \\ m\angle E=100 \end{gathered}[/tex]Answer:
100
Which of the following is only true sometimes? A. The sum of a rational number and a rational number is rational. B. The sum of a rational number and an irrational number is irrational. C. The product of an irrational number and an irrational number is irrational. D. The product of a nonzero rational number and an irrational number is irrational.
Answers
The sum of a rational number and a rational number is rational. ALWAYS
The sum of a rational number and an irrational number is irrational.
The product of an irrational number and an irrational number is irrational. SOMETIMES
For example, the product of multiplicative inverses like √2 and 1/√2 will be 1
The product of a nonzero rational number and an irrational number is irrational.
Find sinif cos 0 = is in the first quadrant. 5 OA. OB. OC. 2/20 OD. 25/ M5 Reset Selection
Answers
Answer: B. 3/5
This question can be solved by using trigonometric identities.
Write an equation for the linear function f(x) using the given information. ———————————————Using the points 2,0 & 4,3
Answers
To find the equation in the form
[tex]y=mx+b[/tex]the slope is defined by:
[tex]\begin{gathered} m=\frac{y2-y1}{x2-x1} \\ m=\frac{3-0}{4-2} \\ m=\frac{3}{2} \end{gathered}[/tex]To find b you can replace any of the points on the equation an clear for b
(x,y)=(4,3)
[tex]\begin{gathered} y=\frac{3}{2}x+b \\ 3=\frac{3}{2}\cdot4+b \\ 3=6+b \\ 3-6=b \\ b=-3 \end{gathered}[/tex]to check if the answer is correct replace 2 as x in the equation.
[tex]\begin{gathered} y=\frac{3}{2}\cdot2-3 \\ y=3-3 \\ y=0 \end{gathered}[/tex]since the answer was 0 and point was 2,0 the equation is correct.
How long does it take Tina to type 864 words, if she took 15 minutes to type out an assignment that comprised 720 words?
Answers
Given data:
The given time taken by Tin to type 720 words is t=15 min.
The given expression can be wriiten as,
720 word=15 min
720 words= 15(60 sec)
720 words= 900 sec
1 word = 900/720 sec
=1.25 sec
Multiplying the above equation with 864 on both sides .
864 words= 864(1.25) sec
= 1080 sec
=1080/60 min
= 18 min.
Thus, the time taken bby Tine to type 864 words is 18 min.
determine the area of figure round to the nearest tenth if necessary..
Answers
select all reasons that support one or more statements in ghe proof.
Answers
Answer:
B, C, D and E.
Explanation:
The proof and reasons for each step is given below:
Step 1:
Statement: RSTU is a parallelogram.
Reason: Given
Step 2:
Statement: RS is parallel to TU and RU is parallel to TS
Reason: (B)Definition of a parallelogram
Step 3:
Statement: ∠RSU≅∠TUS and ∠RUS≅∠TSU.
Reason: (C)Alternate Interior angles are congruent
Step 4:
Statement: SU≅US.
Reason: (E)corresponding parts of congruent triangles are congruent.
Step 5:
Statement: Triangle RSU≅Triangle TUS.
Reason: AAS Congruence Theorem
Step 6:
Statement: RS≅TU and RU≅TS
Reason: (D)Opposite sides of a parallelogram are congruent.
The reasons that support the proof are B, C, D and E.
Find x, for which 7x+8=4x-10
Answers
We are given the equation 7x+8=4x-10 and we want to find the value of x, such that the equality holds. To do so, we will start with the equation and the solve it for x. That is, we will apply mathematical operations on both sides of the equation, so we end up "ilosating" the x on one side of the equality sign. We start by
[tex]7x+8=4x\text{ - 10}[/tex]First, we subtract 4x on both sides, so we get
[tex]\text{ -10=(7x-4x)+8=3x+8}[/tex]Now, we subtract 8 on both sides, so we get
[tex]3x=\text{ -10-8=-18}[/tex]Finally, we divide both sides by 3, so we get
[tex]x=\frac{\text{ -18}}{3}=\text{ -6}[/tex]so x=-6.
What is the product of 0.976 and 1.2
Answers
r is the midpoint of op and qr is perpendicular to op in the diagram below find the the length of qr
Answers
Given:
OP = 20 in
QP = 26 in
Since R is the midpoint of OP, then, OR = RP
Thus
[tex]OR=RP=\frac{OP}{2}=\frac{20}{2}=10\text{ in}[/tex]To find the length of QR, use pythagoras theorem below:
[tex]\begin{gathered} a^2+b^2=c^2 \\ \\ RP^2+QR^2=PQ^2 \end{gathered}[/tex]Input values into the formula:
[tex]10^2+QR^2=26^2[/tex]Subtract 10² from both sides:
[tex]\begin{gathered} 10^2-10^2+QR^2=26^2-10^2 \\ \\ QR^2=26^2-10^2 \end{gathered}[/tex]Take the square root of both sides:
[tex]\begin{gathered} \sqrt[]{QR^2}=\sqrt[]{26^2-10^2} \\ \\ QR=\sqrt[]{676-100} \\ \\ QR=\sqrt[]{576} \\ \\ QR=24 \end{gathered}[/tex]Therefore, the length of QR is 24 in
Fill in the blank with the correct inequality symbol. State which property of inequalities is being utilized.If x-8>10, then x_18.
Answers
GIVEN
The inequality:
[tex]x-8>10[/tex]SOLUTION
The inequality is to be solved.
Add 8 to both sides of the inequality. This follows the Addition Property of Inequalities:
[tex]if\text{ }xTherefore:[tex]\begin{gathered} x-8+8>10+8 \\ x>18 \end{gathered}[/tex]ANSWER
[tex]x>18[/tex]the length of the rectangle is two feet less than 3 times the width.if the area is 65ft^2.find the dimension.
Answers
Given:
The area of the rectangle, A=65ft^2.
Let l be the length of the rectangle and w be the width of the rectangle.
It is given that the length of the rectangle is two feet less than 3 times the width.
Hence, the expression for the length of the rectangle is,
[tex]l=3w-2\text{ ----(A)}[/tex]Now, the expression for the area of the rectangle can be written as,
[tex]\begin{gathered} A=\text{length}\times width \\ A=l\times w \\ A=(3w-2)\times w \\ A=3w^2-2w \end{gathered}[/tex]Since A=65ft^2, we get
[tex]\begin{gathered} 65=3w^2-2w \\ 3w^2-2w-65=0\text{ ---(1)} \end{gathered}[/tex]Equation (1) is similar to a quadratic equation given by,
[tex]aw^2+bw+c=0\text{ ---(2)}[/tex]Comparing equations (1) and (2), we get a=3, b=-2 and c=-65.
Using discriminant method, the solution of equation (1) is,
[tex]\begin{gathered} w=\frac{-b\pm\sqrt[]{^{}b^2-4ac}}{2a} \\ w=\frac{-(-2)\pm\sqrt[]{(-2)^2-4\times3\times(-65)}}{2\times3} \\ w=\frac{2\pm\sqrt[]{4^{}+780}}{2\times3} \\ w=\frac{2\pm\sqrt[]{784}}{6} \\ w=\frac{2\pm28}{6} \end{gathered}[/tex]Since w cannot be negative, we consider only the positive value for w. Hence,
[tex]\begin{gathered} w=\frac{2+28}{6} \\ w=\frac{30}{6} \\ w=5\text{ ft} \end{gathered}[/tex]Now, put w=5 in equation (A) to obtain the value of l.
[tex]\begin{gathered} l=3w-2 \\ =3\times5-2 \\ =15-2 \\ =13ft \end{gathered}[/tex]Therefore, the length of the rectangle is l=13 ft and the width is w=5 ft.
Find the distance between the following points using the pythagorean theorem (5,10) and (10,12)
Answers
Answer:
\sqrt[29]
Explanation:
Given the coordinate (5,10) and (10, 12). The formula for calculating the distance between two points is expressed as;
[tex]D\text{ =}\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}^{}[/tex]Given that;
x1 = 5
y1 = 10
x2 = 10
y2 = 12
Substitute:
[tex]\begin{gathered} D\text{ = }\sqrt[]{(10-5)^2+(12-10)^2} \\ D=\text{ }\sqrt[]{5^2+2^2} \\ D\text{ =}\sqrt[]{25+4} \\ D\text{ =}\sqrt[]{29} \end{gathered}[/tex]Hence the distance between the points is \sqrt[29]
In a garden, there are 10 rows and 12 columns of mango trees. The distance between two trees is 2 meters and a distance of one meter is left from all sides of the boundary of the garden. What is the length of the garden?
Answers
Answer:
20m
Step-by-step explanation:
(10-1)x2+1x2=20m
Part A: The Sun that produces 3.9 * 10^33ergs of a radiant energy per second. How many eggs of radiant energy does the Sun produce and 3.25 * 10^3 seconds?Part B: Which is more the reasonable measurement of the distance between the tracks on a railroad: 1.435 * 10^3mm or 1.435 * 10^3mm?
Answers
Part A
[tex]1.2675\times10^{37}ergs[/tex]Explanations:The sun can produce 3.9 * 10^33 ergs of radiant energy per second
[tex]\text{Amount of energy in 1 second = 3.9 }\times10^{33}ergs[/tex][tex]\text{Amount of energy produced in 3.25}\times10^3\sec \text{ = (3.9}\times10^{33}\times3.25\times10^3)[/tex][tex]\text{Amount of energy produced in 3.25}\times10^3\text{ seconds = }1.2675\times10^{37}ergs[/tex]Paula will make fruit punch for a party she will mix 1 1/2 gallons of orange juice with 5/8 of a gallon of pineapple juice how many 1/8 gallon servings will Paula have
Answers
First let's find the total number of gallons of the fruit punch. To do so, we just need to sum the gallons of orange juice (1 1/2) ith the gallons of pineapple juice (5/8):
[tex]1\frac{1}{2}+\frac{5}{8}=\frac{3}{2}+\frac{5}{8}=\frac{12}{8}+\frac{5}{8}=\frac{17}{8}[/tex]Now, in order to find how many 1/8 servings can be made, we need to divide the total number of gallons of the fruit punch by the number of gallons of a serving:
[tex]\frac{\frac{17}{8}}{\frac{1}{8}}=\frac{17}{8}\cdot\frac{8}{1}=17[/tex]So Paula can have 17 servings.
Answer:
17
Step-by-step explanation:
5/8 - 5
1 1/2 - 12
- Polynomial Functions -For each function, state the vertex; whether the vertex is a maximum or minimum point; the equation of the axis of symmetry and whether the function's graph is steeper than, flatter than, or the same shape as the graph of f(x)=x²
Answers
EXPLANATION
Given the function f(x) = (x-6)^2 + 1
[tex]\mathrm{The\: vertex\: of\: an\: up-down\: facing\: parabola\: of\: the\: form}\: y=ax^2+bx+c\: \mathrm{is}\: x_v=-\frac{b}{2a}[/tex]Expanding (x-6)^2 + 1 by applying the Perfect Square Formula:
[tex]=x^2-12x+37[/tex][tex]\mathrm{The\: parabola\: params\: are\colon}[/tex][tex]a=1,\: b=-12,\: c=37[/tex][tex]x_v=-\frac{b}{2a}[/tex][tex]x_v=-\frac{\left(-12\right)}{2\cdot\:1}[/tex][tex]\mathrm{Simplify}[/tex][tex]x_v=6[/tex][tex]y_v=6^2-12\cdot\: 6+37[/tex]Simplify:
[tex]y_v=1[/tex][tex]\mathrm{Therefore\: the\: parabola\: vertex\: is}[/tex][tex]\mleft(6,\: 1\mright)[/tex][tex]\mathrm{If}\: a<0,\: \mathrm{then\: the\: vertex\: is\: a\: maximum\: value}[/tex][tex]\mathrm{If}\: a>0,\: \mathrm{then\: the\: vertex\: is\: a\: minimum\: value}[/tex][tex]a=1[/tex][tex]\mathrm{Minimum}\mleft(6,\: 1\mright)[/tex][tex]\mathrm{For\: a\: parabola\: in\: standard\: form}\: y=ax^2+bx+c\: \mathrm{the\: axis\: of\: symmetry\: is\: the\: vertical\: line\: that\: goes\: through\: the\: vertex}\: x=\frac{-b}{2a}[/tex]Expanding (x-6)^2 + 1 by applying the Perfect Square Formula:
[tex]y=x^2-12x+37[/tex][tex]\mathrm{Axis\: of\: Symmetry\: for}\: y=ax^2+bx+c\: \mathrm{is}\: x=\frac{-b}{2a}[/tex][tex]a=1,\: b=-12[/tex][tex]x=\frac{-\left(-12\right)}{2\cdot\:1}[/tex][tex]\mathrm{Refine}[/tex]Axis of simmetry : x=6
The quadratic function has the same shape than the parent function y=x^2 because there is NOT a coefficient within x.
Consider the following expression 9x+4y + 1 Select all of the true statements below 1 is a constant. 9x and 1 are like terms. 9x is a factor, 9x + 4y + 1 is written as a sum of three terms. ( 9x is a coefficient. None of these are true.
Answers
ANSWER:
1st option: 1 is a constant
4th option: 9x + 4y + 1 written as a sum of three terms
STEP-BY-STEP EXPLANATION:
We have the following equation:
[tex]9x+4y+1[/tex]From the following equation we can say the following:
• The only constant term is 1
,• None of the terms are similar
,• There are a total of 3 terms
,• The coefficients are 9 and 4
,• The factors are 9, 4, 1, x and y
From the above we can affirm that the true statements are:
• 1 is a constant
• 9x + 4y + 1 written as a sum of three terms
P(B) = 2/3P(An B) = 1/6What will P(A) have to be for A and B to be independent?1/211/121/45/6
Answers
P(B) = 2/3
P(An B) = 1/6
What will P(A) have to be for A and B to be independent?
Remember that
Events A and B are independent if the equation P(A∩B) = P(A) · P(B) holds true
substitute given values
1/6=P(A)*(2/3)
solve for P(A)
P(A)=1/4Simplify the following expression. Assume variables are positive. Express your answer using rational exponents.
Answers
Let's simplify the expression:
[tex]\begin{gathered} (x^{-\frac{1}{2}}\cdot y^{-\frac{2}{3}}\cdot z^{-2})^{-\frac{1}{2}}=x^{(-\frac{1}{2})(-\frac{1}{2})}y^{(-\frac{2}{3})(-\frac{1}{2})}z^{(-2)(-\frac{1}{2})} \\ =x^{\frac{1}{4}}y^{\frac{1}{3}}z \end{gathered}[/tex]Therefore the answer is:
[tex]x^{\frac{1}{4}}y^{\frac{1}{3}}z[/tex]Consider the equation cos(2t) = 0.8. Find the smallest positive solution in radians and round your answer to 2 decimal places.
Answers
Given:
cos(2t) = 0.8
Take the cos⁻' of both-side of the equation.
cos⁻' cos(2t) = cos⁻'(0.8)
2t = cos⁻'(0.8)
Calculate the value of the right- hand side with your calculator in radians.
2t =0.6435
Divide both-side of the equation by 2
t ≈ 0.32
Solve for x. 8x-2x+7>21+10
Answers
Answer: [tex]x > 4[/tex]
Step-by-step explanation:
[tex]8x-2x+7 > 21+10\\\\6x+7 > 31\\\\6x > 24\\\\x > 4[/tex]
−1= 8x+2i need help with this problem,
Answers
Given
-1 = 8x + 2
Answer
-1 = 8x + 2
-1 -2 =8x
-3 = 8x
x = -3/8
Find an angle θ with 0∘<θ<360∘that has the same:
Sine as 80∘ : θ = ______ degrees
Cosine as 80∘ : θ = _____ degrees
Answers
Answer:
sin80° = sin100°
cos80° = cos280°
Step-by-step explanation:
In general, sin(a)° = sin (180-a)° and cos(a)° = cos(360-a)°
How much money would you have if you deposited $100.00 in an account thatearned 8% interest after 20 years?
Answers
Problem:
How much money would you have if you deposited $100.00 in an account that earned 8% interest after 20 years?.
Solution:
Step 1: Calculate 8% of the given amount ($100.00):
[tex]100.00\text{ x 0.08 = \$8 }[/tex]Step 2: Add the above value to the money deposited:
$100.0 + $8 = $108.0
Thus, we can conclude that the money in this account after 20 years is $108.0
What is 10/12 written in simplest form?
Answers
ANSWER:
[tex]\frac{5}{6}[/tex]STEP-BY-STEP EXPLANATION:
We have the following fraction
[tex]\frac{10}{12}[/tex]Now to reduce to its simplest form, we must simplify
[tex]\frac{2\cdot5}{2\cdot6}=\frac{5}{6}[/tex]The ages of three siblings, Ben, Bob and Billy, are consecutive integers. The square of the age of the youngest child Ben is four more than eight times the age of the oldest child, Billy. How old are the three boys?
Answers
Let the age of the youngest child (Ben) be x years.
Since the ages are consecutive integers, the ages of the other 2 are (x + 1) and (x + 2).
It was given that the age of the youngest child is four more than eight times the age of the oldest child. This means that:
[tex]x^2-4=8(x+2)[/tex]We can rearrange the equation above and solve for x as a quadratic equation:
[tex]\begin{gathered} x^2-4=8x+16 \\ x^2-8x-20=0 \end{gathered}[/tex]Using the factorization method, we have:
[tex]\begin{gathered} x^2-10x+2x-20=0 \\ x(x-10)+2(x-10)=0 \\ (x-10)(x+2)=0 \\ \therefore \\ x-10=0,x+2=0 \\ x=10,x=-2 \end{gathered}[/tex]Since the age cannot be negative, the age of the youngest child is 10.
Therefore, the ages are:
[tex]\begin{gathered} Ben=10\text{ }years \\ Bob=11\text{ }years \\ Billy=12\text{ }years \end{gathered}[/tex]