A student attempted to solve the system 5x + 2y = 10 and 10x + 2y = 1 by graphing. The graph and the conclusion are
below. What can you say about the student's work?
y
-10x + 2y = 1
5x + 2y = 10
The soluion is ().
O The solution is incorrect because the student did not correctly identify the intersection.
O The solution is correct and the lines are graphed correctly.
O The solution is correct, but the lines were graphed incorrectly.
O The solution is incorrect because the lines are not graphed correctly.
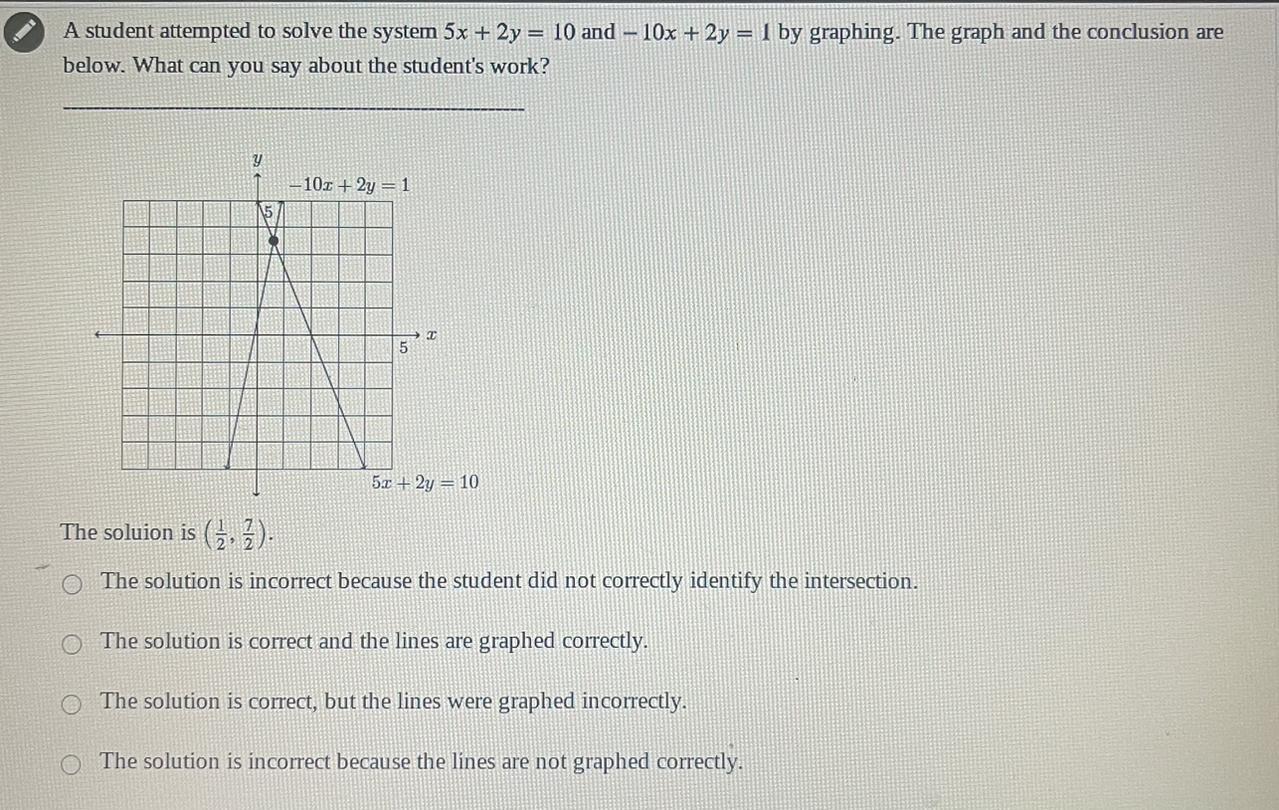
Answers
Answer:
Option A: The solution is incorrect because the student did not correctly identify the intersection.
Step-by-step explanation:
Solve by elimination method.
5x + 2y = 10; -10x + 2y = 1
Multiply the second equation by -1, then add the equations together.
(5x + 2y = 10)
-1 (-10x + 2y = 1)
Forms:
5x + 2y = 10
10x - 2y = -1
Add these equations to eliminate y.
15x = 9
Then solve 15x = 9 for x:
15x = 9
15/15 = 9/15 (Divide both sides by 15)
x = 3/5
Now that we've found x let's plug it back in to solve for y.
Write down the original equation:
5x + 2y = 10
Substitute 3/5 for x in:
5x + 2y = 10:
5(3/4)+2y=10
2y+3=10
2y+3-3=10+-3
2y=7
2y/2 = 7/2
y = 7/2
x = 3/5 and y = 7/2.
Comparing the identified answers to the one found by the students, it can be concluded that Option A: The solution is incorrect because the student did not correctly identify the intersection.
Related Questions
On the Y axis, we have the profit from the trucking company and on the X axis, we have the miles the truck has traveled. The company decided that they needed to start paying for a driver at a price of 0.25 cents a mile. After this change what will happen to the x and y axis/slope?
A. Y intercept will be less and X will be less
B. Y intercept will be less and X intercept will be greater
C. Y intercept will be greater and X will be greater
D. Y intercept will be greater and X will be less
Answers
The correct answer is: A. Y intercept will be less and X will be less.
What is slope?A linear function's slope is a gauge of how steep the line is. Between any two points on the line, it is the ratio of the change in the y-coordinate to the change in the x-coordinate. The formula is used to compute it:
slope equals (y2 - y1)/. (x2 - x1)
where any two points on the line (x1, y1) and (x2, y2) are.
The company's expenses will rise once it begins paying a driver at a rate of 0.25 cents per mile, which means its profit will decline. The profit curve on the y-axis will go vertically downward as a result of this. But, because the cost of paying the driver is fixed per mile and has no impact on the profit per mile, the slope of the line—which reflects the profit per mile—will stay the same.
Hence, A. Y intercept will be less and X will be less is correct.
Learn more about slope here:
https://brainly.com/question/19131126
#SPJ1
Brenda is fishing from a small boat. Her fishing hook is 12 feet below her, and a fish is swimming at the same depth as the hook, 16 feet away. How far away is Brenda from the fish?
Answers
Answer:
We can use the Pythagorean theorem to solve this problem. Let's call the distance Brenda is away from the fish "x". Then, we have a right triangle with legs of length 12 and x, and a hypotenuse of length 16. So:
x^2 + 12^2 = 16^2
Simplifying:
x^2 + 144 = 256
x^2 = 112
Taking the square root of both sides:
x ≈ 10.6 feet
Therefore, Brenda is approximately 10.6 feet away from the fish.
what is the ratio between yellow to red?
6 yellow = 5 green
4 green = 3 purple
5 purple = 2 red
A.3 to 1
B.4 to 1
C.5 to 1
D.6 to 1
Answers
The ratio between yellow to red is 1 to 2 or 1:2. Answer: not listed.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
First, we can use the given information to find the ratio between green and yellow:
6 yellow = 5 green
=> green/yellow = 6/5
Next, we can use the given information to find the ratio between purple and green:
4 green = 3 purple
=> purple/green = 4/3
Finally, we can use the given information to find the ratio between red and purple:
5 purple = 2 red
=> red/purple = 5/2
To find the ratio between yellow and red, we can combine these ratios and simplify:
green/yellow = 6/5
=> yellow/green = 5/6
purple/green = 4/3
=> green/purple = 3/4
red/purple = 5/2
=> purple/red = 2/5
yellow/green * green/purple * purple/red = yellow/red
(5/6) * (3/4) * (2/5) = 1/2
Therefore, the ratio between yellow to red is 1 to 2 or 1:2. Answer: not listed.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
Let u = 4i-j, v = 5i + j. and w=i+6j.
Find the specified scalar
U*V+U*W
Answers
To find the specified scalar, we need to first find the dot product of U and V, and then the dot product of U and W, and add these two dot products together:
U·V + U·W
where U·V denotes the dot product of U and V, and U·W denotes the dot product of U and W.
The dot product of two vectors a = (a1, a2) and b = (b1, b2) is given by:
a · b = a1b1 + a2b2
Using this formula, we can find the dot product of U and V:
U · V = (4i - j) · (5i + j) = 4i · 5i + 4i · j - j · 5i - j · j = 20i^2 + (4i · j - 5i · j) - j^2 = 20 + (-i · j) - 1 = 19 - i · j
Next, we can find the dot product of U and W:
U · W = (4i - j) · (i + 6j) = 4i · i + 4i · 6j - j · i - j · 6j = 4i^2 + (4i · 6j - j · i) - 6j^2 = 4 + (24i · j) - 6 = -2 + 24i · j
Now we can substitute these values into the original expression:
U·V + U·W = (19 - i·j) + (-2 + 24i·j) = 17 + 23i·j
Therefore, the specified scalar is 17 + 23i·j.
PLSSS HELP ME ITS DUE TOMORROW!!!!!
Answers
^4√p7
in exponential form.
Answers
Answer:1111
Step-by-step explanation:
Find the value of x. Write your answer in simplest form.
Answers
Answer:
C
Step-by-step explanation:
using the sine ratio and the exact value
sin45° = [tex]\frac{1}{\sqrt{2} }[/tex] , then
sin45° = [tex]\frac{opposite}{hypotenuse}[/tex] = [tex]\frac{5}{x}[/tex] = [tex]\frac{1}{\sqrt{2} }[/tex] ( cross- multiply )
x = 5[tex]\sqrt{2}[/tex]
What is the least whole number that rounds to 570 when rounded to the nearest ten?
What is the greatest whole number that rounds to 570 when rounded to the nearest ten?
Use the number pad to enter your answers in the boxes.
Least number:
Greatest number:
Answers
Answer:
Least: 565
Greatest: 574
Step-by-step explanation:
564 would round down to 560 and 575 would round to 580
Helping in the name of Jeus.
The least whole number that rounds to 570 when rounded to the nearest ten is 570. The greatest whole number that rounds to 570 when rounded to the nearest ten is 580.
Explanation:To find the least whole number that rounds to 570 when rounded to the nearest ten, we need to look at the digit in the tens place. In this case, the tens digit is 7. Since the number can only round up or down, we need to determine if rounding 570 to the nearest ten would be up or down. Since 570 is closer to 570 than to 580, we can round down to 570. Therefore, the least whole number that rounds to 570 when rounded to the nearest ten is 570 itself.
On the other hand, to find the greatest whole number that rounds to 570 when rounded to the nearest ten, we again need to look at the digit in the tens place. Since the tens digit is 7, we need to determine if rounding 570 to the nearest ten would be up or down. Since 570 is closer to 580 than to 570, we can round up to 580. Therefore, the greatest whole number that rounds to 570 when rounded to the nearest ten is 580.
Learn more about rounding here:
https://brainly.com/question/34045884
#SPJ2
Hello, I am confused on how to answer this question.
Answers
Answer: x=14
Step-by-step explanation:
cb=10.
ac=14
The value of X will be 14.
This is a simple mathematics problem that can be solved by using ratios.
Given, AC : BC : AB = 7 : 5 : 8
AC = X ; BC = 10 ; AB = X + 2
AC/ BC = X/ 10 = 7/5 (Ratios can also be represented as fractions)
X/10 = 7/5
On Transposing,
5X = 70
X = 70/5
X = 14
Alternatively,
BC/AB = 5/8 = 10/ (X + 2)
5/8 = 10/ (X + 2)
On Transposing,
80 = 5X + 10
5X = 70
X = 14
To know more about Ratios,
https://brainly.com/question/29442975
4. This number line
number of minutes Diane read
week for 3 weeks.
0
200
100
300
How many minutes did she read after
the first week?
minutes
After the second week?
After the third week?
minutes
minutes
How many minutes did she read each
week? Explain how you know.
5. Diane reads the same number of minutes
each week. How many minutes does
she read after 4 weeks? After 5 weeks?
Skip count on the number line above to
find the answers.
After 4 weeks:
After 5 weeks:
minutes
minutes
Answers
4) Dane read an average of 400 minutes per week. 5) Diane will have read 2000 minutes after 5 weeks.
How to determine how many minutes did she read each week4) The number "0200100300" represents the number of minutes Diane read each week for 3 weeks. To find out how many minutes she read after the first week, we simply look at the first digit, which is "0." This means that Diane did not read any minutes during the first week.
To find out how many minutes she read after the second week, we add the digits in the first two positions, which are "02." This gives us a total of 2 x 60 = 120 minutes.
To find out how many minutes she read after the third week, we add the digits in the first three positions, which are "020." This gives us a total of 20 x 60 = 1200 minutes.
To find out how many minutes she read each week, we simply divide the total number of minutes by the number of weeks, which is 3. So Diane read a total of 1200 minutes in 3 weeks, which means she read an average of 400 minutes per week.
5) If Diane reads the same number of minutes each week, then she will read that same number of minutes after 4 weeks and after 5 weeks. To find out how many minutes she reads after 4 weeks, we can skip count by the same number repeatedly: 400, 800, 1200, 1600. So Diane will have read 1600 minutes after 4 weeks.
Similarly, to find out how many minutes she reads after 5 weeks, we can skip count again by the same number repeatedly: 400, 800, 1200, 1600, 2000. So Diane will have read 2000 minutes after 5 weeks.
Learn more about minutes per week at https://brainly.com/question/30756043
#SPJ1
Write an Algebraic Equation for each problem (include a let statement) and use it to solve the world problem
On number is eight less than five times another. If the the sum of the two numbers is 28, find the two numbers.
The smaller number is __.
The larger number is __.
Answers
The smaller number is 6 .
The larger number is 22
To solve this problem
Let's let x be the smaller number and y be the larger number.
From the problem, we know that one number is eight less than five times the other, so we can write:
y = 5x - 8
We also know that the sum of the two numbers is 28, so we can write:
x + y = 28
Now we have two equations in two variables. We can solve for one of the variables in terms of the other, and substitute that expression into the other equation to eliminate one variable.
Let's solve the first equation for x
x = (y + 8)/5
Now we can substitute this expression for x into the second equation:
(y + 8)/5 + y = 28
Multiplying both sides by 5 to eliminate the fraction, we get:
y + 8 + 5y = 140
Combining like terms, we get:
6y + 8 = 140
Subtracting 8 from both sides, we get:
6y = 132
Dividing both sides by 6, we get:
y = 22
Now we can use the equation y = 5x - 8 to solve for x:
22 = 5x - 8
Adding 8 to both sides, we get:
30 = 5x
Dividing both sides by 5, we get:
x = 6
Therefore, the smaller number is 6 and the larger number is 22.
Learn more about Algebraic Equation here : brainly.com/question/24875240
#SPJ1
ANSWER Quick Due in 5 minutes!!!!!!
The line plots represent data collected on the travel times to school from two groups of 15 students. A horizontal line starting at 0, with tick marks every two units up to 28. The line is labeled Minutes Traveled. There is one dot above 4,6,14, and 28. There are two dots above 10, 12, 18, and 22. There are three dots above 16. The graph is titled Bus 47 Travel Times. A horizontal line starting at 0, with tick marks every two units up to 28. The line is labeled Minutes Traveled. There is one dot above 8, 9,18, 20, and 22. There are two dots above 6, 10, 12,14, and 16. The graph is titled Bus 18 Travel Times. Compare the data and use the correct measure of variability to determine which bus is the most consistent. Explain your answer. Bus 18, with an IQR of 16 Bus 47, with an IQR of 24 Bus 18, with a range of 16 Bus 47, with a range of 24
Answers
IQR offers a more accurate indicator of consistency than range since it is less impacted by outliers.
Due to Bus 18's smaller IQR, we can infer that it is more consistent than Bus 47.
WHAT IS IQR?An indicator of statistical dispersion used to describe the variability of a dataset is the interquartile range (IQR). It is derived by subtracting a dataset's 75th percentile (Q3) from its 25th percentile (Q1). When compared to other measures of variability like range, the IQR represents the middle 50% of the data and is less susceptible to outliers.
We must contrast the measurements of variability for the two buses in order to determine which one is more reliable. We can utilize range and interquartile range as measurements of variability. (IQR).
The range of a dataset is the difference between its maximum and minimum values.
The range for Bus 18 is 16 (22 - 6), whereas the range for Bus 47 is 24. (28 - 4).
As a result, Bus 47's range is greater than Bus 18's.A measure of variability that is less impacted by outliers than the range is the interquartile range (IQR). It is determined as the difference between a dataset's third and first quartiles (Q3 and Q1, respectively).
The IQR is 16 for Bus 18 (Q3 - Q1 = 22 - 6)
The IQR for Bus 47 is 24 (Q3 - Q1 = 28 - 4"). Bus 18 therefore has a lower IQR than Bus 47.IQR offers a more accurate indicator of consistency than range since it is less impacted by outliers. Due to Bus 18's smaller IQR, we can infer that it is more consistent than Bus 47.
To know more about interquartile range visit:
brainly.com/question/29204101
#SPJ1
A ski club charges $70 for a lift ticket and $20 per hour to ski. Jim paid at least $130 last week to ski. How many hours would he have skied.
Answers
Answer:
Step-by-step explanation: $130-$70 lift = $60/$20 per hour= 3 hours ski time
70+20=90
90+20=110
110+20=130
Matt can save $225 per month that he puts into a savings
account earning 5% annual interest. How much will he have
saved after 2 years?
Answers
Answer:
FV ≈ $5,673.56
Step-by-step explanation:
To calculate the total amount that Matt will have saved after 2 years of saving $225 per month at an annual interest rate of 5%, we can use the formula for the future value of an annuity:
FV = P * (((1 + r/12)^(n*12) - 1) / (r/12))
where:
FV is the future value of the annuity
P is the periodic payment (in this case, $225 per month)
r is the interest rate per year (in this case, 5%)
n is the number of years (in this case, 2)
Substituting the given values, we get:
FV = $225 * (((1 + 0.05/12)^(2*12) - 1) / (0.05/12))
Using a calculator, we get:
FV ≈ $5,673.56
Therefore, after 2 years of saving $225 per month at an annual interest rate of 5%, Matt will have saved approximately $5,673.56.
You own 23 CDs. You want to randomly arrange 5 of them in a CD rack. What is the probability that the rack ends up in alphabetical order?
The probability that the CDs are in alphabetical order is
Answers
The probability of choosing 5 CDs in alphabetical order out of a collection of 23 CDs is approximately 0.00003 or 0.003%.
What is combination?
In mathematics, a combination is a way of selecting objects from a larger group of objects, where the order of selection is not important. A combination is a subset of objects that are chosen from a larger set without regard to the order in which they are selected.
The formula is given by:
C(n, r) = [tex]\frac{n!}{r!* (n - r)!}[/tex]
The total number of ways to choose 5 CDs from a collection of 23 CDs is given by the combination formula:
C(23, 5) = [tex]\frac{23!}{5!* (23 - 5)!}[/tex]
= 33649
This means there are 33649 different ways to arrange 5 CDs out of the 23 CDs.
Out of these 33649 ways, only one arrangement is alphabetical. For this to happen, the first CD chosen must be the first one alphabetically, the second CD chosen must be the second one alphabetically, and so on.
The first CD can be any of the 23 CDs. However, once the first CD is chosen, there is only one CD that can be the second one alphabetically, two CDs that can be the third one alphabetically, and so on. Therefore, the probability of choosing 5 CDs in alphabetical order is:
P = 1 / C(23, 5)
P = 1 / 33649
P ≈ 0.00003
So the probability of choosing 5 CDs in alphabetical order out of a collection of 23 CDs is approximately 0.00003 or 0.003%.
To learn more about combination visit the link:
https://brainly.com/question/11732255
#SPJ1
Given cos A = 3/10 and tan A < 0 , find sin A .
Answers
Answer: Since we know that cos A = 3/10, we can use the Pythagorean identity to find sin A:
sin^2 A + cos^2 A = 1
sin^2 A = 1 - cos^2 A
sin A = sqrt(1 - cos^2 A)
Substituting cos A = 3/10, we get:
sin A = sqrt(1 - (3/10)^2)
sin A = sqrt(1 - 9/100)
sin A = sqrt(91)/10
Since we also know that tan A < 0, we know that the sine and tangent of A have opposite signs, and therefore sin A is negative.
Therefore:
sin A = -sqrt(91)/10
Step-by-step explanation:
This pattern follows the rule add 2. What is another feature of this pattern? (4 points) An image of a pattern. Term one has one dot, term two has three dots, term three has five dots, term four has seven dots. a The terms appear even, odd, even, odd. b All the terms are even. c Two terms are even, then two terms are odd. d All the terms are odd.
Answers
The correct answer is c: Two terms are even, then two terms are odd. This pattern follows the rule of adding 2, so each successive term is an even number followed by an odd number.
Number is a mathematical object used to count, measure and represent a quantity. It is used to symbolize a numerical quantity or value, and is used in various ways in mathematics, science, engineering, finance and other fields. Numbers are also used to represent relationships between objects, such as the number of sides in a triangle or the number of students in a classroom.
This alternating pattern of even and odd terms is a feature of the pattern, with two terms being even followed by two terms being odd. This pattern continues as the terms increase, with the even terms adding 2 and the odd terms adding 2 as well. This pattern is a good way to remember a sequence of numbers and can be used to help understand patterns in mathematics.
To know more about number click-
http://brainly.com/question/24644930
#SPJ1
What’s the length of side AB?
Answers
tan = 1/√3= perpendicular/ base
1/√3 = AB / AC
AB / 6 = 1/√3
AB = 6/√3
Class: Algebra 2
I need help with these Natural Logarithms problems!!!!!
I will give lots of points!!!!
Answers
The solutions are: x = ln(2) for 2eˣ = 4, x = ln(25)/4 for e⁴ˣ = 25, x = ln(72) for eˣ = 72 and x = ln(124)/3 for e³ˣ = 124.
Solving equations using natural logarithmTo solve these equations using natural logarithm, we can use the following rules:
If a = eᵇ, then b = ln(a).If ln(aᵇ) = b ln(a).Using these rules, we can solve the given equations as follows:
2eˣ = 4
Divide both sides by 2 to get
eˣ = 2.
Take the natural logarithm of both sides to get
ln(eˣ) = ln(2).
Using rule 1 above, we can simplify ln(eˣ) to x, and we get
x = ln(2).
e⁴ˣ = 25
4x = ln(25).
Divide both sides by 4 to get
x = ln(25)/4.
eˣ = 72
Take the natural logarithm of both sides to get
x = ln(72).
e³ˣ = 124
Take the natural logarithm of both sides to get
3x = ln(124).
Divide both sides by 3 to get
x = ln(124)/3.
For the second set of equations, we use the same rule as above
So, we have
ln(x - 3) = 2
x - 3 = e²
x = e² + 3.
x ≈ 10.389.
Therefore, the solution is x ≈ 10.389.
ln(2t) = 4
2t = e⁴
t = 0.5 * e⁴
t ≈ 27.299.
Therefore, the solution is t ≈ 27.299.
Read more about logarithm at
https://brainly.com/question/24160402
#SPJ1
A random sale of 40 flower shop customers was surveyed to find customers' favorite flowers. The table shows the results. The shop expects to sell 50 bunches of flowers on Sunday. How many bunches of each flower should the shop order?
Answers
Answer:
below
Step-by-step explanation:
To find out how many bunches of each flower the shop should order, we need to calculate the percentage of customers who preferred each flower, and then use that percentage to estimate the number of bunches needed for each flower.
First, we need to calculate the total number of customers who were surveyed:
Total customers surveyed = 8 + 4 + 8 + 20 = 40
Next, we can calculate the percentage of customers who preferred each flower:
Percentage of customers who preferred daisy = (8/40) x 100% = 20%
Percentage of customers who preferred gardenia = (4/40) x 100% = 10%
Percentage of customers who preferred mum = (8/40) x 100% = 20%
Percentage of customers who preferred rose = (20/40) x 100% = 50%
Now, we can use these percentages to estimate how many bunches of each flower to order.
Let's assume that each bunch contains 10 flowers (this is just an example, the actual number may vary):
Number of bunches of daisy to order = 20% of 50 bunches = 10 bunches
Number of bunches of gardenia to order = 10% of 50 bunches = 5 bunches
Number of bunches of mum to order = 20% of 50 bunches = 10 bunches
Number of bunches of rose to order = 50% of 50 bunches = 25 bunches
So, the shop should order 10 bunches of daisy, 5 bunches of gardenia, 10 bunches of mum, and 25 bunches of rose to meet the expected demand on Sunday.
There is a 25% chance that a vowel is drawn from a bag of random letter tiles. what is the probability of drawing a vowel, placing it back in the bag, and then drawing a consonant
Answers
The probability of drawing a vowel, placing it back in the bag, and then drawing a consonant is 0.1875 or 18.75%.
Calculating the probability
The probability of drawing a vowel from the bag of random letter tiles is 25%. Since the tile is replaced after drawing, the probability of drawing a vowel on the second draw is also 25%.
The probability of drawing a vowel and then a consonant can be calculated by multiplying the probabilities of each event:
P(vowel and consonant) = P(vowel) x P(consonant)
= 0.25 x 0.75
= 0.1875
Read more about probability at
https://brainly.com/question/251701
#SPJ1
4. Assuming that the rectangles have whole number side lengths, why is it possible to draw two different rectangles that have an area of 30 square inches but not possible to draw two rectangles with an area of 7 square inches?
Answers
Answer:
hm
Step-by-step explanation:
The reason why it is possible to draw two different rectangles that have an area of 30 square inches is that there are multiple pairs of whole numbers that multiply to 30. For example, a rectangle with dimensions 5 inches by 6 inches has an area of 30 square inches, and so does a rectangle with dimensions 2 inches by 15 inches.
However, the number 7 is a prime number, which means it can only be divided evenly by 1 and itself. Therefore, the only way to get an area of 7 square inches for a rectangle is by multiplying 1 and 7, which means the dimensions of the rectangle would be 1 inch by 7 inches. Since there are no other pairs of whole numbers that multiply to 7, it is not possible to draw two different rectangles with an area of 7 square inches.
Hurry please combine Leon’s results and Celia’s results to find the experimental probability of spinning a 4
Answers
The experimental probability of spinning a 4 will equals to 0.3.
How to find the experimental probability of spinning a 4?Outcome Tally Frequency
1 IIII 4
2 III 3
3 IIIIIIII 7
4 IIIIII 6
Total 20
The probability of spinning a 4:
= 6/20
= 3/10
= 0.3
Read more about probability
brainly.com/question/24756209
#SPJ1
At a local play, student tickets cost $6 each and adult tickets cost $11 each. If ticket sales were $3,000 for 400 tickets, how many students attended the play?
120
180
220
280
Answers
Answer:
If ticket sales were $3,000 for 400 tickets then 280 students attended the play.
Step-by-step explanation:
Which is NOT the same as asking:
What is the logarithm of 1,296 if the base is 6?
Answers
Reason: log=exponent, so whenever you see a log, that means you’re solving for an exponent.
A hamster runs at a speed of 16 centimeters per second in a wheel of radius 15 centimeters.
a) What is the angular velocity of the wheel? (in radians/sec)
b) How fast will the wheel spin in revolutions per minute?
Answers
a) The angular velocity of the wheel is approximately 1.0667 radians per second. b) The wheel will spin at approximately 10.16 revolutions per minute.
What is angular velocity?Angular velocity is a measure of how quickly an object rotates or revolves around a fixed point, such as an axis or a center of rotation. It is a vector quantity that describes the rate of change of an object's angular position with respect to time, and is usually expressed in units of radians per second (rad/s) or degrees per second (deg/s).
According to given information:a) To find the angular velocity of the wheel, we can use the formula:
angular velocity = linear velocity / radius
In this case, the linear velocity of the hamster is 16 centimeters per second, and the radius of the wheel is 15 centimeters. So, we have:
angular velocity = 16 / 15
angular velocity = 1.0667 radians per second
Therefore, the angular velocity of the wheel is approximately 1.0667 radians per second.
b) To find the speed of the wheel in revolutions per minute, we need to convert the angular velocity from radians per second to revolutions per minute. There are 2π radians in one revolution, and 60 seconds in one minute. So, we can use the following formula:
angular velocity (in revolutions per minute) = angular velocity (in radians per second) * 60 / 2π
Plugging in the angular velocity we found in part (a), we get:
angular velocity (in revolutions per minute) = 1.0667 * 60 / 2π
angular velocity (in revolutions per minute) ≈ 10.16 revolutions per minute
Therefore, the wheel will spin at approximately 10.16 revolutions per minute.
To know more about angular velocity visit:
https://brainly.com/question/15154527
#SPJ1
A rectangular flower bed measures 10m by 6m. It has a path 2m
wide around it. Find the area of the path
Answers
The area of the path is 80 square meters.
Given: A rectangular flower bed measures 10m by 6m. It has a path 2m wide around it.
To Find: The area of the path.
Solution: We need to subtract the area of the inner rectangle from the area of the outer rectangle.
So,
The outer rectangle has dimensions 14m by 10m (adding 2m to each side of the flower bed), so its area is:
A outer = 14m x 10m = 140 m²
Now,
The inner rectangle has dimensions 10m by 6m (the original dimensions of the flower bed), so its area is.
A inner = 10m x 6m = 60 m²
Now,
The area of the path.
A path = A outer - A inner
= 140 m² - 60 m²
= 80 m²
Thus, The area of the path is 80 square meters.
Learn more about rectangles here:
https://brainly.com/question/15019502
FIND THR CIRCUMFERENCE OF A CD THAT HAS A RADIUS OF 6 CENTIMETERS
___cm
Answers
Answer:
Hm
Step-by-step explanation:
The formula to find the circumference of a circle is:
Circumference = 2πr
Where "r" is the radius of the circle, and "π" (pi) is a mathematical constant approximately equal to 3.14.
Substituting the given value of radius, we get:
Circumference = 2 x π x 6
Circumference = 12π
Circumference ≈ 37.7 cm (rounded to one decimal place)
Therefore, the circumference of a CD that has a radius of 6 centimeters is approximately 37.7 cm.
what is one of the zeros of the function shown in this graph?
Answers
Answer:
x = -3 and x = 1 are the two zeroes of this function. Choose one of them for your answer.
Triangle PQR is rotated 180 degrees clockwise about the origin to produce the image Triangle P’Q’R’. Which of the following statements is TRUE abóyate Triangle P’Q’R’.
Answers
Answer:
Step-by-step explanation:
We get triangle PQR by plotting the point P (1, 4), Q (3, 1), R (2, -1) on the graph paper when rotated through 180° about the origin. The new position of the point is: P (1, 4) → P' (-1, -4) Q (3, 1) → Q' (-3, -1) R (2, -1) → R' (-2, 1) Thus, the new position of ∆PQR is ∆P’Q’R’.