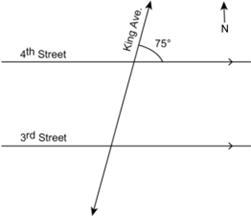
1. All numbered streets runs parallel to each other. Both 3rd and 4th Streets are intersected by King Ave. as shown:
(a) Suppose a car is traveling east on 4th Street and turns onto King Avenue heading northeast. What is the measure of the angle created by the car's turning? Explain your answer.
(b) Suppose a car is traveling southwest on King Avenue and turns left onto 3rd Street. What is the measure of the angle created by the car's turning? Explain your answer.
(c) Suppose a car is traveling northeast on King Avenue and turns right onto 3rd Street. What is the measure of the angle created by the car's turning? Explain your answer.
Answers
When the car travels east on 4th Street and turns onto King Avenue heading northeast, the angle created by the car's turning is a 45-degree angle.
When the car travels southwest on King Avenue and turns left onto 3rd Street, the angle created by the car's turning is a 135-degree angle.
When the car travels northeast on King Avenue and turns right onto 3rd Street, the angle created by the car's turning is a 45-degree angle.
How to get the Angle?(a) When the car travels east on 4th Street and turns onto King Avenue heading northeast, the angle created by the car's turning is a 45-degree angle. This is because the intersection of 4th Street and King Avenue creates a right angle, and the car turns northeast, creating another 45-degree angle with the horizontal 4th Street.
(b) When the car travels southwest on King Avenue and turns left onto 3rd Street, the angle created by the car's turning is a 135-degree angle. This is because the intersection of King Avenue and 3rd Street creates a right angle, and the car turns left, creating an additional 90-degree angle. Therefore, the total angle is 90 degrees + 45 degrees = 135 degrees.
(c) When the car travels northeast on King Avenue and turns right onto 3rd Street, the angle created by the car's turning is a 45-degree angle. This is because the intersection of King Avenue and 3rd Street creates a right angle, and the car turns right, creating another 45-degree angle with the horizontal 3rd Street.
Learn more about right angle here: https://brainly.com/question/29869536
#SPJ1
Related Questions
Aeronautical researchers have developed three different processes to pack a parachute. They want to compare the different processes in terms of time to deploy and reliability. There are 1,200 objects that they can drop with a parachute from a plane. Using a table of random digits, the researchers will randomly place the 1,200 items into three equally sized treatment groups suitable for comparison. Which design is the most appropriate for this experiment
- Randomly number each item with 1, 2, or 3. Assign the items labeled 1 to the process 1 group, assign the items labeled 2 to the process 2 group, and assign the items labeled 3 to the process 3 group.
- Number each item from 1 to 1,200.
Reading from left to right from a table of random digits, identify 800 unique numbers from 1 to 1,200. Assign the items with labels in the first 400 numbers to the process 1 group. Assign the items with labels in the second 400 numbers to the process 2 group. Assign the remaining items to the process 3 group.
- Number each item from 0000 to 1199.
Reading from left to right on a random number table, identify 800 unique four-digit numbers from 0000 to 1199. Assign the items with labels in the first 400 numbers to the process 1 group. Assign the items with labels in the second 400 numbers to the process 2 group. Assign the remaining items to the process 3 group.
- Select an item, and identify the first digit reading from left to right on a random number table. If the first digit is a 1, 2, or 3, assign the item to the process 1 group.
If the first digit is a 4, 5, or 6, assign the item to the process 2 group. If the first digit is a 7, 8, or 9, assign the item to the process 3 group. If the first digit is a 0, skip that digit and move to the next one to assign the item to a group. Repeat this process for each item.
Answers
Answer: The most appropriate design for this experiment is the third option:
- Number each item from 0000 to 1199.
- Reading from left to right on a random number table, identify 800 unique four-digit numbers from 0000 to 1199. Assign the items with labels in the first 400 numbers to the process 1 group. Assign the items with labels in the second 400 numbers to the process 2 group. Assign the remaining items to the process 3 group.
This design ensures that the groups are equally sized and selected randomly without any biases. The use of a random number table to assign the groups helps to avoid any systematic patterns or preferences that might arise from numbering or labeling the items directly.
Step-by-step explanation:
The count in a bateria culture was initially 300, and after 35 minutes the population had increased to 1600. Find the doubling period. Find the population after 70 minutes. When will the population reach 10000?
Answers
doubling time = (ln 2) / r
where r is the exponential growth rate.
Using the given information, we can calculate the exponential growth rate as:
r = (ln N1 - ln N0) / t
where N0 is the initial population, N1 is the final population, and t is the time elapsed. Plugging in the values, we get:
r = (ln 1600 - ln 300) / 35
r = 0.5128
Now we can calculate the doubling period as:
doubling time = (ln 2) / r
doubling time = (ln 2) / 0.5128
doubling time = 1.35 hours (rounded to two decimal places)
Therefore, the doubling period is approximately 1.35 hours.
To find the population after 70 minutes, we can use the formula for exponential growth:
N = N0 * e^(rt)
Plugging in the values, we get:
N = 300 * e^(0.5128 * (70/60))
N = 1467.05
Therefore, the population after 70 minutes is approximately 1467.05.
To find when the population will reach 10000, we can use the same formula again:
N = N0 * e^(rt)
Plugging in the given values, we get:
10000 = 300 * e^(0.5128 * t)
Dividing both sides by 300, we get:
e^(0.5128 * t) = 10000 / 300
e^(0.5128 * t) = 33.3333
Taking the natural logarithm of both sides, we get:
0.5128 * t = ln(33.3333)
t = ln(33.3333) / 0.5128
t = 23.37 hours (rounded to two decimal places)
Therefore, the population will reach 10000 after approximately 23.37 hours.
Given F(x) = 4x - 8 and g(x) = -3x + 1, what is (f - g)(x)?
A) 7x-9
B) 7x - 7
C) x-9
D) x - 7
Answers
Therefore, the answer is (A) 7x-9 when it is given that function F(x) = 4x - 8 and g(x) = -3x + 1.
What is function?In mathematics, a function is a relationship between two sets of values, where each input (or domain element) is associated with a unique output (or range element). In other words, a function is a rule or a process that takes an input (or inputs) and produces a corresponding output. Functions can be expressed using various mathematical notations, such as algebraic formulas, graphs, tables, or even verbal descriptions. They are widely used in many fields of mathematics, science, engineering, economics, and computer science, to model and solve problems that involve relationships between variables or quantities.
Here,
To find (f - g)(x), we need to subtract g(x) from f(x), so we get:
(f - g)(x) = f(x) - g(x)
Substituting the given functions, we get:
(f - g)(x) = (4x - 8) - (-3x + 1)
Simplifying the expression by distributing the negative sign, we get:
(f - g)(x) = 4x - 8 + 3x - 1
Combining like terms, we get:
(f - g)(x) = 7x - 9
To know more about function,
https://brainly.com/question/28193995
#SPJ1
$2000 are invested in a bank account at an interest rate of 5 percent per year.
Find the amount in the bank after 7 years if interest is compounded annually.
Find the amount in the bank after 7 years if interest is compounded quaterly.
Find the amount in the bank after 7 years if interest is compounded monthly.
Finally, find the amount in the bank after 7 years if interest is compounded continuously.
Answers
The amount in the bank after 7 years increases as the compounding frequency increases, and it is highest when interest is compounded continuously.
Simple interest calculation.
Using the formula A = P(1 + r/n)^(nt), where:
A = the amount in the account after t years
P = the principal (initial amount)
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded per year
t = the number of years
a) If interest is compounded annually:
A = 2000(1 + 0.05/1)^(1*7) = $2,835.08
b) If interest is compounded quarterly:
A = 2000(1 + 0.05/4)^(4*7) = $2,888.95
c) If interest is compounded monthly:
A = 2000(1 + 0.05/12)^(12*7) = $2,905.03
d) If interest is compounded continuously:
A = Pe^(rt) = 2000e^(0.05*7) = $2,938.36
Therefore, the amount in the bank after 7 years increases as the compounding frequency increases, and it is highest when interest is compounded continuously.
Learn more about simple interest below.
https://brainly.com/question/25793394
#SPJ1
Help me on this problem!
Answers
use pythagoras theorem to do 15^2 - 9^2=144 and the square root of that is 12
I need helppp!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Answers
Answer:
Step-by-step explanation:
The distance formula is
[tex]d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}[/tex]
x1 is a,
x2 is 0,
y1 is 0 and
y2 is b. Fitting those into the formula where they belong:
[tex]d=\sqrt{(0-a)^2+(b-0)^2}[/tex] and
[tex]d=\sqrt{(-a)^2+(b)^2}[/tex]
Since a negative squared is a positive, then
[tex]d=\sqrt{a^2+b^2}[/tex]
which is the second choice down.
Name one right angle.
Name one straight angle.
Answers
Straight angle: DEF
what’s the surface area of this figure ?
Answers
Thus, the total surface area of pentagonal prism is found to be 308.6 sq. ft.
Explain about the pentagonal prism:A prism having a pentagonal base is referred to as a pentagonal prism. It has two hexagonal bases, five parallelogram faces, and seven faces. Seven faces, fifteen edges, and ten vertices make up a pentagonal prism.
The two bases of each of the seven faces—two pentagons—and the remaining five faces—parallelograms—connect the bases of the pentagons.
Given data:
base area B = 84.3 sq. ftLength of rectangular side L = 7 ftwidth of rectangular side w = 4 ftsurface area of pentagonal prism = 2* base area + 5*rectangle area
surface area of pentagonal prism = 2* B + 5*L*w
surface area of pentagonal prism = 2* 84.3 + 5*7*4
surface area of pentagonal prism = 168.6 + 140
surface area of pentagonal prism = 308.6 sq. ft
Thus, the total surface area of pentagonal prism is found to be 308.6 sq. ft.
Know more about the pentagonal prism:
https://brainly.com/question/15637173
#SPJ1
the area of Rectangle is 112 in sq. if the height is 8 in, what is the base length
Answers
Answer:
14cm
Step-by-step explanation:
112÷8=14
base length=14cm
Answer:
To find the base length of a rectangle, given its area and height, you can use the formula for calculating the area of a rectangle, which is:
Area = Length x Width
In this case, you are given that the area is 112 square inches and the height is 8 inches. Let's denote the base length as "x" inches.
So, the equation for the area of the rectangle becomes:
112 = x * 8
To solve for "x", you can divide both sides of the equation by 8:
112 / 8 = x
x = 14
Therefore, the base length of the rectangle is 14 inches.
11. Triangles can be classified by their side lengths or by their angle measures. Sometimes triangles are classified using both classifications (side length and angle measure) but these can be redundant and unnecessary. Give an example of a classification based on both side length and angle measure that is unnecessary and explain why.
Answers
By answering the presented question, we may conclude that As a result, adding the isosceles triangle categorization is superfluous and redundant in this circumstance.
What is triangle?A triangle is a polygon since it has three sides and three vertices. It is a basic geometric shape. Triangle ABC refers to a triangle with the vertices A, B, and C. In Euclidean geometry, a single plane and triangle are obtained when the three points are not collinear. If a triangle has three sides and three corners, it is a polygon. The triangle's corners are the spots where the three sides meet. The sum of three triangle angles equals 180 degrees.
An isosceles triangle has two sides of equal length, but a right triangle has one angle that measures 90 degrees. As a result, an isosceles right triangle is one with two equal-length sides and one 90-degree angle.
The Pythagorean theorem states that in any right triangle, the two legs (the sides next to the right angle) are always of equal length. Hence, if we know that a triangle has one 90-degree angle and two equal-length sides, we already know that it is a right triangle and that the two legs are equal. As a result, adding the isosceles triangle categorization is superfluous and redundant in this circumstance.
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
Part of the proceeds from a garage sale was $290 worth of $5 and $20 bills. If there were 8 more $5 bills than $20 bills, find the number of each denomination.
Answers
Answer:
18 5-dollar bills
10 20-dollar bills
the 3rd and 6th term in fibonacci sequence are 7 and 31 respectively find the 1st and 2nd terms of the sequence
Answers
Answer:
Step-by-step explanation:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144,233,377,610,987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, ... Can you figure out the next few numbers?
Factorize the following polynomials:
1) 54x²+42x³ - 30x4
Answers
54x² + 42x³ - 30x4
= 6x²(9 + 7x - 5x²)
Now, we can factor the expression in parentheses using the quadratic formula or by factoring it as a product of two binomials:
9 + 7x - 5x² = (3 - x)(3 + 5x)
Therefore, we have:
54x² + 42x³ - 30x4 = 6x²(3 - x)(3 + 5x)
So the factored form of the polynomial 54x²+42x³ - 30x4 is 6x²(3 - x)(3 + 5x).
An average newspaper contains at least 9 pages and at most 46 pages. How many newspapers must be collected to be certain that at least two newspapers have the same number of pages?
Answers
We need to collect 46 newspapers to be certain that at least two newspapers have the same number of pages.
What is the minimum number of newspapers needed to guarantee that two newspapers have the same number of pages?According to the Pigeonhole Principle, if we have n+1 pigeons and n holes, then there must be at least one hole with two or more pigeons. Similarly, if we have n+1 newspapers with n possible page counts, then there must be at least one page count that appears in two or more newspapers.
In this case, we have a range of 38 possible page counts (46 - 9 + 1), so we need at least 39 newspapers to guarantee that each possible page count appears in at least one newspaper.
However, to guarantee that at least two newspapers have the same number of pages, we need one more newspaper than the number of possible page counts, so we need a total of 46 newspapers. Therefore, if we collect 46 newspapers, we can be certain that at least two of them have the same number of pages.
Read more about newspapers
brainly.com/question/28171687
#SPJ1
KPI Payouts are: Prepaid Ring-out Only: $ 1.00 Prepaid Activation: $ 2.00 Accessories: 1.5 Equipment Protection: $ 1.00 You can make $ and ring it out at the POS. % when you activate a prepaid device with equipment protection
Answers
If no accessories are sold, $3 will be paid out. In the event that accessories are sold, the compensation is $2.00 plus $1.00 plus 1.5 percent of their worth.
Based on the information given, the KPI payouts are:
$1.00 for each Prepaid Ring-out Only
$2.00 for each Prepaid Activation
1.5% of the value of each Accessories sale
$1.00 for each Equipment Protection sale
We need to know the values of the prepaid activation and equipment protection in order to compute the payment for activating a prepaid device with equipment protection. Assume that the equipment protection is worth $Y and the prepaid activation is worth $X.
The following would be the total payment for activating a prepaid device with equipment protection:
Payout = $2.00 (for activation) + $1.00 (for equipment protection) + 1.5% (of the value of accessories sold)
If no accessories are sold, the payout would be:
Payout = $2.00 + $1.00
= $3.00
If accessories worth $Z are also sold, the payout would be:
Payout = $2.00 + $1.00 + 1.5% of $Z
= $2.00 + $1.00 + 0.015Z
So the payout for activating a prepaid device with equipment protection depends on the value of the accessories sold.
Therefore, If no accessories are sold, the payout is $3.00. If accessories are sold, the payout is $2.00 + $1.00 + 1.5% of the value of the accessories sold.
To learn more about Percentage from the given link.
brainly.com/question/29967647
#SPJ1
You take out a loan in the amount of your tuition and fees cost $70,000. The loan has a monthly interest rate of 0.25% and a monthly payment of $250. How long will it take you to pay off the loan? Use the formula N= (-log(1-i*A/P))/(log(1+i)) to determine the number of months it will take you to pay off the loan. Let N represent the number of monthly payments that will need to be made, i represent the interest rate in decimal form, A represent the amount owed (total amount of the loan), and P represent the amount of your monthly payment. Be sure to show your work for all calculations made.
Answers
Therefore, it will take 173 months to pay off the loan, or approximately 14 years and 5 months.
What is percentage?A percentage is a way of expressing a number as a fraction of 100. The symbol for a percentage is "%". For example, 50% is the same as 50/100 or 0.5 as a decimal. Percentages are often used to express a portion or share of a whole. For instance, if you scored 90% on a test, it means you got 90 out of 100 possible points. In finance, percentages are commonly used to express interest rates, returns on investments, or changes in stock prices.
First, we need to convert the monthly interest rate from a percentage to a decimal by dividing by 100.
0.25% / 100 = 0.0025
Now we can plug in the values into the formula:
N= (-log (1-0.0025*70000/250))/ (log (1+0.0025))
Simplifying the equation in the parentheses:
N= (-log (1-175))/ (log (1.0025))
N= (-log (0.9964))/ (0.002499)
N= 172.9
Rounding up to the nearest whole number since we can't make partial payments:
N= 173
To learn more about percentage, visit
https://brainly.com/question/29306119
#SPJ1
Which of these expressions could Alex and Taylor use to calculate the square footage of the tile Dining area? Find only the tile floor, and not the cabinets shown in black. Select all that apply.
A 34 foot by 13 foot grid. The kitchen is flush left. It has an 18 foot by 2 foot horizontal rectangle in the top left of the grid. Under the far left and right sides of the rectangle are two 6 foot by 2 foot vertical rectangles. There are two other horizontal rectangles on the bottom left of the grid that are 2 foot by 6 foot. There is a 4 foot gap between them. The dining room is on the right with a 12 foot by 2 foot rectangle in the top right of the grid.
Select answers
(16 x 13) - (12 x 2)
(4 x 13) + (12 x 2) + (12 x 11)
(17 x 11) + (4 x 2)
(4 x 13) + (12 x 11)
Answers
Expressions for the square footage of the tile Dining area, Considering only the tile floor, and not the cabinets shown in black will be (16 x 13) - (12 x 2) and (4 x 13) + (12 x 11)
How to calculate the area of rectangle?The area of a rectangle is a measure of the amount of space it occupies in two-dimensional (2D) space. It is calculated by multiplying the length of the rectangle by its width. Mathmatically,
[tex]Area=length*width[/tex]
Now, Solving given problem,
The total area of the grid will be:Length of grid = 16 ft, Width of grid = 13 ft
Total area of grid = Length x Width = 16 ft x 13 ft = 208 sq ft
The area of the rectangle in the top right :Length of rectangle = 12 ft, Width of rectangle = 2 ft
Area of rectangle = Length x Width = 12 ft x 2 ft = 24 sq ft
To remove the top right rectangle from the tile dining area, subtract its area from the total area of the grid:
(Total area of grid) - (Area of rectangle in top right) = (208 sq ft -24 sq ft )= 184 sq ft
So, the expression for this calculation will be: (16 x 13) - (12 x 2) = 184 sq ft
The area of the vertical rectangles on the far left and right sides is calculated as follows:Width of vertical rectangles = 4 ft, Length of grid = 13 ft
Area of vertical rectangles = Width of vertical rectangles x Length of grid = 4 ft x 13 ft = 52 sq ft
The area of the rectangle in the top right:Length of rectangle = 12 ft, Width of rectangle = 11 ft
Area of rectangle = Length x Width = 12 ft x 11 ft = 132 sq ft
Add the areas of the vertical rectangles and the rectangle in the top right to get the total area of the tile dining area:
Area of vertical rectangles + Area of rectangle in top right = 52 sq ft + 132 sq ft = 184 sq ft
So, the expression for this calculation is: (4 x 13) + (12 x 11) = 184 sq ft
Hence, both of these expressions- (16 x 13) - (12 x 2) and (4 x 13) + (12 x 11) gives the square footage of the tile dining area based on the given information.
Learn more about Areas here:
https://brainly.com/question/27683633
#SPJ1
Is each number rounded correctly to the nearest hundred thousand?
Answers
yes is answer for all option .we can check it by rules of rounding off numbers .
what is rounding ?
Rounding is the process of approximating a number to a nearby value that is easier to work with or more appropriate for a given context. When rounding, we take a number with many decimal places or significant figures and adjust it to a simpler or more convenient value with fewer decimal places or significant figures.
In the given question,
Yes, each number is rounded correctly to the nearest hundred thousand based on the rules of rounding.
To round to the nearest hundred thousand, we look at the digit in the hundred thousand place and the digit to its right (i.e., in the ten thousand place).
If the digit in the ten thousand place is 5 or greater, we round up the digit in the hundred thousand place by adding 1.
If the digit in the ten thousand place is less than 5, we leave the digit in the hundred thousand place as it is.
Using these rules, we can see that:
350000 rounded to the nearest hundred thousand is 400000 because the digit in the ten thousand place is 5, so we round up the digit in the hundred thousand place.
555555 rounded to the nearest hundred thousand is 560000 because the digit in the ten thousand place is 5, so we round up the digit in the hundred thousand place.
137998 rounded to the nearest hundred thousand is 200000 because the digit in the ten thousand place is 7, so we round up the digit in the hundred thousand place.
792314 rounded to the nearest hundred thousand is 800000 because the digit in the ten thousand place is 3, so we leave the digit in the hundred thousand place as it is.
To know more about rounding , visit:
https://brainly.com/question/29878750
#SPJ1
The reflector of a flashlight is in the shape of a paraboloid of revolution. Its diameter is 8 centimeters and its depth is 4 centimeters. How far from the vertex should the light bulb be placed so that the rays will be reflected parallel to the axis?
Answers
Answe: The distance of light bulb can be calculated using equation of parabola. The parabola is a plane curve which is U-shaped.
Step-by-step explanation:
The following data values represent a population. What is the variance of the population? u = 12. Use the information in the table to help you.
A. 18 B. 41 O C. 12 OD. 80
x 3 11 13 21
(x-μ)² 81 1 1 81
Answers
The variance of the population according to the given table is option B 41.
What is variance?The spread or dispersion of a set of data around its mean is measured by variance. It has the same units as the original data and is calculated as the average of the squared deviations from the mean. Variance is a frequently used statistical term to describe the diversity or variability of a population or sample. When the variance is modest, the data points are closely grouped around the mean, whereas when the variance is great, the data points are widely dispersed.
The variance is given by the formula:
variance = (sum of squared deviations from the mean) / (number of observations)
Using the table we have sum of squared deviations from the mean:
81 + 1 + 1 + 81 = 164
variance = 164 / 4 = 41
Hence, the variance of the population according to the given table is option B 41.
Learn more about variance here:
https://brainly.com/question/13708253
#SPJ1
Please help with this math question!
Answers
The exponential function of the population is P(x) = 15000 * 1.046^x
Calculating the exponential function of the populationFrom the question, we have the following parameters that can be used in our computation:
Initial, a = 15000
Rate, r = 4.6%
The equation of the function is represented as
P(x) = a * (1 + r)^x
Substitute the known values in the above equation, so, we have the following representation
P(x) = 15000 * (1 + 4.6%)^x
Evaluate
P(x) = 15000 * 1.046^x
Hence, the function is P(x) = 15000 * 1.046^x
Read more about exponential function at
https://brainly.com/question/2456547
#SPJ1
Please I’ll give brainliest
A Ferris wheel reaches a maximum height of 60 m above the ground and takes twelve minutes to complete one revolution. Riders have to climb a m staircase to board the ride at its lowest point.
(a) [4 marks] Write a sine function for the height of Emma, who is at the very top of the ride when t = 0.
(b) [2 marks] Write a cosine function for Eva, who is just boarding the ride.
(c) (2 marks] Write a sine function for Matthew, who is on his way up, and is at the same height as the central axle of the wheel.
Answers
If Riders have to climb a m staircase to board the ride at its lowest point.
a. sine function for the height of Emma, who is at the very top of the ride when t = 0 is: h(t) = 60 sin(π/6 t).
b. a cosine function for Eva, who is just boarding the ride is: h(t) = m + 60 cos(π/6 t).
c. a sine function for Matthew is: h(t) = 30 sin(π/6 t).
What is the sine function for the height of Emma?(a) Let's assume that the Ferris wheel completes one full revolution in 12 minutes. The height of the Ferris wheel can be modeled by a sine function as it moves up and down periodically. When the Ferris wheel completes one revolution, it returns to its original position, so the period of the sine function is 12 minutes.
The maximum height of the Ferris wheel is 60 m, so the amplitude of the sine function is 60 m. When t = 0, Emma is at the very top of the ride, which means she is at the maximum height of the Ferris wheel. Therefore, the sine function for Emma's height, h(t), can be written as:
h(t) = 60 sin(2π/12 t)
Simplifying this equation, we get:
h(t) = 60 sin(π/6 t)
(b) Eva is just boarding the ride, which means she is at the lowest point of the ride when t = 0. The cosine function is ideal for modeling this situation, as it starts at its maximum value and reaches its minimum value after one-fourth of the period. Therefore, the cosine function for Eva's height, h(t), can be written as:
h(t) = m + 60 cos(2π/12 t)
Simplifying this equation, we get:
h(t) = m + 60 cos(π/6 t)
where m is the height of the staircase that Eva has to climb to board the ride.
(c) Matthew is at the same height as the central axle of the Ferris wheel, which means he is halfway between the maximum and minimum height of the ride. Therefore, the sine function for Matthew's height, h(t), can be written as:
h(t) = 30 sin(2π/12 t)
Simplifying this equation, we get:
h(t) = 30 sin(π/6 t)
Therefore sine function for the height of Emma, who is at the very top of the ride when t = 0 is: h(t) = 60 sin(π/6 t).
Learn more about sine function here:https://brainly.com/question/9565966
#SPJ1
In a bag there are 3 red marbles, 2 yellow marbles, and 1 blue marble. What is the likelihood of a yellow marble being selected on the first draw?
likely
unlikely
even chance
certain
Answers
Therefore, it is not even chance, but it is also not very unlikely. It is moderately likely that a yellow marble will be selected on the first draw.
What is Probability?Probability is a branch of mathematics that deals with the study of random events and their likelihood of occurring. It is a measure of the likelihood or chance of an event happening. Probability is expressed as a number between 0 and 1, where 0 means the event is impossible, and 1 means the event is certain.
In other words, probability is a way of quantifying uncertainty. It is used in various fields, such as statistics, physics, finance, engineering, and more, to help make predictions and decisions based on uncertain information. Probability theory provides a set of rules and tools for analyzing and manipulating random variables and events, and for calculating the probability of complex events.
The likelihood of a yellow marble being selected on the first draw can be calculated by dividing the number of yellow marbles by the total number of marbles in the bag:
likelihood of selecting a yellow marble = number of yellow marbles / total number of marbles
So, in this case, the likelihood of selecting a yellow marble on the first draw is:
likelihood of selecting a yellow marble = 2 / (3 + 2 + 1) = 2/6 = 1/3
To know more about probability visit:
https://brainly.com/question/30034780
#SPJ1
The five number summary of a dataset was found to be:
45, 52, 56, 63, 66
An observation is considered an outlier if it is below:
An observation is considered an outlier if it is above:
Answers
An observation is considered an outlier if it is below 35.5 or above 79.5 in this dataset.
Identifying the outliers in the summaryTo determine the outliers in a dataset using the five-number summary, we need to calculate the interquartile range (IQR), which is the difference between the third quartile (Q3) and the first quartile (Q1).
IQR = Q3 - Q1
Where
Q1 = 52
Q3 = 63
So, we have
IQR = 63 - 52
IQR = 11
An observation is considered an outlier if it is:
Below Q1 - 1.5 × IQR
Above Q3 + 1.5 × IQR
Substituting the values, we get:
Below 52 - 1.5 × 11 = 35.5
Above 63 + 1.5 × 11 = 79.5
Therefore, an observation is considered an outlier if it is below 35.5 or above 79.5 in this dataset.
Read more about outliers at
https://brainly.com/question/27893355
#SPJ1
Angel made a table runner that has an area of 80 square inches. The length and width of the table runner are whole numbers. The length is 5 times greater than the width. What are the dimensions of the table runner?
Answers
the dimensions of the table runner are [tex]20[/tex] inches in length and [tex]4[/tex] inches in width.
What are the dimensions?Let's denote the width of the table runner as "w" inches. Since the length is 5 times greater than the width, the length would be 5w inches.
The area of a rectangle is calculated by multiplying its length by its width. Given that the area of the table runner is 80 square inches, we can set up the following equation:
Length × Width = Area
[tex](5w) \imes w = 80[/tex]
Simplifying further:
[tex]5w^2 = 80[/tex]
Dividing both sides by 5:
[tex]w^2 = 16[/tex]
Taking the square root of both sides:
w = ±4
Since the width cannot be negative in this context, we discard the negative value. Therefore, the width (w) of the table runner is [tex]4[/tex] inches.
Substituting this value back into the equation for length:
Length [tex]= 5w = 5 \times 4 = 20[/tex] inches
So, the dimensions of the table runner are [tex]20[/tex] inches in length and 4 inches in width.
Learn more about dimensions here:
https://brainly.com/question/28688567
#SPJ1
A rectangle has an area of 108 square
centimeters. Its width is 9 centimeters.
What is the perimeter of the
rectangle?
Answers
Therefore, the perimeter of the rectangle is 42 centimeters.
What is area?The concept of area is used in many areas of mathematics, science, and everyday life. It is used in geometry to calculate the area of various shapes, such as triangles, circles, and polygons. It is also used in physics to calculate the amount of surface area of an object that is exposed to air or water, and in architecture and engineering to determine the amount of material needed to construct a building or structure.
Here,
To find the perimeter of a rectangle, we need to know its length and width. We are given that the width of the rectangle is 9 centimeters, and the area of the rectangle is 108 square centimeters.
We can use the formula for the area of a rectangle:
Area of rectangle = length x width
Plugging in the values we have:
108cm² = length x 9cm
Solving for the length, we can divide both sides by 9cm:
length = 108cm² / 9cm
length = 12cm
So, the length of the rectangle is 12 centimeters.
To find the perimeter of the rectangle, we can use the formula:
Perimeter of rectangle = 2 x (length + width)
Plugging in the values we have:
Perimeter of rectangle = 2 x (12cm + 9cm)
Perimeter of rectangle = 2 x 21cm
Perimeter of rectangle = 42cm
To know more about area,
https://brainly.com/question/20693059
#SPJ1
what is 15 to the power of 12
Answers
Answer:
1.2974634e+14
Step-by-step explanation:
ye
What are answers to these questions?
1. f is concave up on the intervals = ?
2. f is concave down on the intervals = ?
3. The inflection points occur at x = ?
Answers
f(x) is concave up on the interval (-∞, √(6/7)) U (√(6/7), ∞),f(x) is concave down on the interval (-√(6/7), √(6/7)) ,The inflection points occur at x = -√(6/7) and x = √(6/7).
What is inflection Point?An inflection point is a point on a curve where the concavity changes, from concave up to concave down or vice versa, indicating a change in the curvature of the curve.
According to the given information:
To determine the intervals where f(x) is concave up or down, we need to find the second derivative of f(x) and determine its sign.
First, we find the first derivative of f(x):
f'(x) = (14x)/(7x²+6)²
Then, we find the second derivative of f(x):
f''(x) = [28(7x²+6)²- 28x(7x²+6)(4x)] / (7x²+6)^4
Simplifying the expression, we get:
f''(x) = 28(42x² - 72) / (7x^2+6)³
To determine where f(x) is concave up or down, we need to find the intervals where f''(x) is positive or negative, respectively.
Setting f''(x) = 0, we get:
42x² - 72 = 0
Solving for x, we get:
x = ±√(6/7)
These are the possible inflection points of f(x). To determine if they are inflection points, we need to check the sign of f''(x) on both sides of each point.
We can use a sign chart to determine the sign of f''(x) on each interval.
Intervals where f''(x) > 0 are where f(x) is concave up, and intervals where f''(x) < 0 are where f(x) is concave down.
Here is the sign chart for f''(x):
x | -∞ | -√(6/7) | √(6/7) | ∞
f''(x)| - | + | - | +
From the sign chart, we can see that:
a) f(x) is concave up on the interval (-∞, √(6/7)) U (√(6/7), ∞).
b) f(x) is concave down on the interval (-sqrt(6/7), √(6/7)).
c) The inflection points occur at x = -√(6/7) and x = √(6/7).
Therefore, the open intervals where f(x) is concave up are (-∞, -√(6/7)) and (√(6/7), ∞), and the open interval where f(x) is concave down is (-√(6/7), √(6/7)). The inflection points occur at x = -√(6/7) and x = √(6/7).
To know more about inflection point visit :
https://brainly.com/question/30760634
#SPJ1
The f(x) is concave up on the interval (-∞, √(6/7)) U (√(6/7), ∞),f(x) is concave down on the interval (-√(6/7), √(6/7)) ,The inflection points occur at x = -√(6/7) and x = √(6/7).
What is inflection Point?
An inflection point is a point on a curve where the concavity changes, from concave up to concave down or vice versa, indicating a change in the curvature of the curve.
According to the given information:
To determine the intervals where f(x) is concave up or down, we need to find the second derivative of f(x) and determine its sign.
First, we find the first derivative of f(x):
f'(x) = (14x)/(7x²+6)²
Then, we find the second derivative of f(x):
f''(x) = [28(7x²+6)²- 28x(7x²+6)(4x)] / (7x²+6)^4
Simplifying the expression, we get:
f''(x) = 28(4x² - 72) / (7x^2+6)³
To determine where f(x) is concave up or down, we need to find the intervals where f''(x) is positive or negative, respectively.
Setting f''(x) = 0, we get:
42x² - 72 = 0
Solving for x, we get:
x = ±√(6/7)
These are the possible inflection points of f(x). To determine if they are inflection points, we need to check the sign of f''(x) on both sides of each point.
We can use a sign chart to determine the sign of f''(x) on each interval.
Intervals where f''(x) > 0 are where f(x) is concave up, and intervals where f''(x) < 0 are where f(x) is concave down.
Here is the sign chart for f''(x):
x | -∞ | -√(6/7) | √(6/7) | ∞
f''(x)| - | + | - | +
From the sign chart, we can see that:
a) f(x) is concave up on the interval (-∞, √(6/7)) U (√(6/7), ∞).
b) f(x) is concave down on the interval (-sqrt(6/7), √(6/7)).
c) The inflection points occur at x = -√(6/7) and x = √(6/7).
Therefore, the open intervals where f(x) is concave up are (-∞, -√(6/7)) and (√(6/7), ∞), and the open interval where f(x) is concave down is (-√(6/7), √(6/7)). The inflection points occur at x = -√(6/7) and x = √(6/7).
To know more about inflection point visit :
https://brainly.com/question/30760634
#SPJ1
HELP FAST PLEASEEE!!!!
Answers
The correct matches for the probability of falling below the z-score are:
-0.08: 0.4681
0.63: 0.7357
-2.7: 0.0035
1.95: 0.9744
Explain probability
Probability is a measure of the likelihood or chance of an event occurring. It is expressed as a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain. Probability is calculated by dividing the number of favourable outcomes by the total number of possible outcomes. Probability is used in many fields, including mathematics, statistics, science, economics, and finance, to make predictions and decisions based on uncertain events.
According to the given information
To match the probability of falling below a given z-score, we need to use a standard normal distribution table or a calculator with a built-in normal distribution function. Here are the probabilities for each z-score:
For a z-score of -0.08, the probability of falling below it is 0.4681.For a z-score of 0.63, the probability of falling below it is 0.7357.For a z-score of -2.7, the probability of falling below it is 0.0035.For a z-score of 1.95, the probability of falling below it is 0.9744.To know more about probability visit
brainly.com/question/11234923
#SPJ1
Find the length of the triangle.
The length of the unknown side of the triangle is __________
Answers
Answer:
The answer is 2√10
Step-by-step explanation:
Hyp²=opp²+adj²
let hyp be x
x²=6²+2²
x²=36+4
x²=40
square root both sides
√x²=√40
x=2√10